적분표(Table of Integrals)

역도함수

구간 I에서 f(x)가 정의된다고 할 때, F(x)를 f(x)의 역도함수(antiderivative)라 하자.

- 구간 I에서 역도함수 F(x)와 f(x)가 정의될 때, f(x)는 역도함수의 도함수로 표현할 수 있다.

 

f(x)는 F(x)의 도함수이다.

 

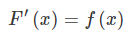
- F(x)는 f(x)의 역도함수로, x∈I를 만족한다.

 

 

F(x) 찾기

예를 들어, x^2(f(x))의 역도함수로 x^3/3이 가능함을 계산할 수 있다.

 

식 1

 

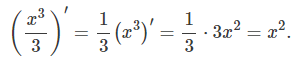
뿐만 아니라 (x^3/3)+5 또는 (x^3/3)-7도 x^2의 역도함수가 됨을 미분표를 활용해 쉽게 확인할 수 있다.

- 상수함수의 도함수는 0이다.

 

+5나 -7은 constant로 C로 일반화하여 표현가능하다.

 

 

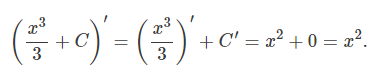
f(x)의 antiderivative는 증명 과정에서 본 것처럼 다양한 constant를 가질 수 있으므로, 역도함수군(the set of all antiderivatives)을 이룬다고 할 수 있으며 이를 함축한 단어로 (역도함수군을) f(x)의 부정적분(indefinite integral)이라 부른다.

 

식 2

 

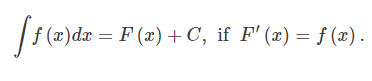
식 1의 내용을 식 2처럼 표현하면 아래와 같다.

 

 

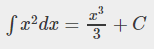
- ∫: integral symbol

- f(x): integrand

- x: variable of integration

- dx: differential of the variable x

- C: constant of integration

 

적분표

러시아의 수학자 I. S. Gradshteyn과 I. M. Ryzhik이 쓴 적분표(Table of Integrals, Series, and Products)는 현재까지 가장 많이 인용되는 수학책 중 하나이다. 

 

네덜란드의 수학자이자 과학역사가였던 David Bierens de Haan(1822~1895)은 수집한 적분식들을 집대성한 저서 『Tables d'intégrales définies』(1858)을 출간했다. 이 책은 이후 Gradshteyn과 Ryzhik의 적분표 제작에 많은 영향을 주었으며, Haan의 저서에서 그대로 인용한 적분식들은 별도로 BI(Bierens)라는 문자로 표기해 두었다.

 

적분은 결과적으로 미분의 역과정이므로, 적분표는 또한 미분표(table of derivatives)의 형태와 유사하다.

- a, p(p≠0), C는 real constant이다.

- b는 지수함수의 밑으로 b>0, b≠1의 조건을 갖는다.

 

 

상수함수의 부정적분

 

 

 

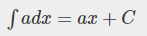
멱의 법칙

- p≠0 and p≠-1

 

 

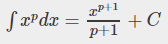
1/x의 부정적분

 

 

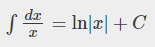
More generally,

 

 

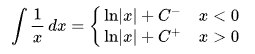
지수함수의 부정적분

 

(1) b^x

 

 

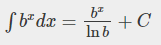
(2) e^x

 

 

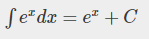
삼각함수의 부정적분

 

 

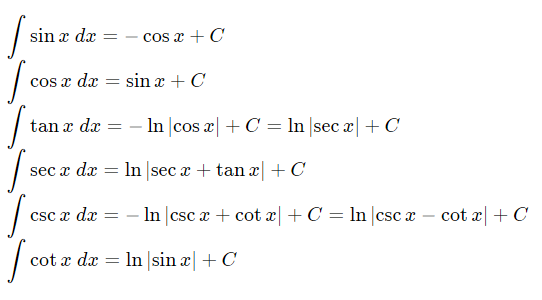
로그함수의 부정적분

 

 

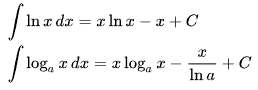
쌍곡선함수의 부정적분