미분표(Table of Derivatives)

미분표

미분적분학 개념에서 다룬 미분식들을 표로 정리하면 다음과 같다.

- C: a constant and real number

- k: a constant and real number

- n: real numbers

- f, g, u, v: the functions with respect to the real variable x

 

f(x), g(x), u(x), v(x)

 

- a: base a of the exponential and logarithmic functions (단, a>0, a≠1 조건(conditions)을 갖는다.)

 

 

상수함수의 도함수

 

 

멱의 법칙(power rule)

 

 

미분에서의 멱의 법칙은 뉴턴과 라이프니츠가 독립적으로 유도(17세기 중반)했다. 한편 적분에서의 멱의 법칙은 이보다 이른 시기(1621년에서 1635년 사이)에 이탈리아의 수학자 보나벤투라의 저서 『불가분량을 사용한 새로운 방법으로 연속체를 설명한 기하학』을 통해 소개되었다.

 

적분에서의 멱의 법칙

 

Bonaventura F. Cavalieri  (1598 ~1647, 이탈리아)

 

 

상수가 곱해진 함수의 도함수

 

 

합법칙과 차법칙

 

 

※ extended sum rule

 

 

곱법칙

 

 

※ extended product rule

 

 

extended product rule에 따라 (uv)''와 (uv)'''을 구할 수 있다.

 

uv 곱함수의 이차 도함수

 

uv 곱함수의 삼차 도함수

 

몫법칙

 

 

역함수(f(x)^-1)의 도함수

 

 

지수함수 도함수

 

 

※ a^x의 도함수와 헷갈리지 않도록 한다!

 

 

로그함수 도함수

 

 

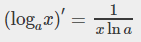
자연로그 도함수

 

 

삼각함수의 도함수

 

 

 

 

 

 

 

연쇄법칙을 사용하면 아래와 같은 삼각함수의 도함수(삼각함수의 응용도함수)도 유도할 수 있다.

 

 

쌍곡선함수의 도함수(Derivatives of Hyperbolic Functions)

 

 

 

각 미분식의 증명(proof)은 미분적분학 개념편에서 확인하도록 하자.