
좌표계 Coordinate Systems
데카르트 좌표계(Cartesian coordinate system): 원점 O를 기준으로 서로 수직인 두 축으로 구분된 이차원 평면
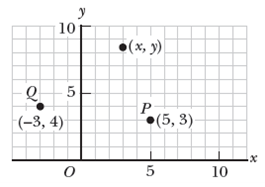
- 또 다른 이름으로는 직각좌표(rectangular coordinate)로 불린다.
- [Fig 1]과 같이 직각좌표의 좌표는 축의 위치에 따라 (x, y)로 표현된다.
- 평면상의 한 점을 표현할 경우 평면극좌표계(plane polar coordinate)를 사용하는 것 또한 편하다.
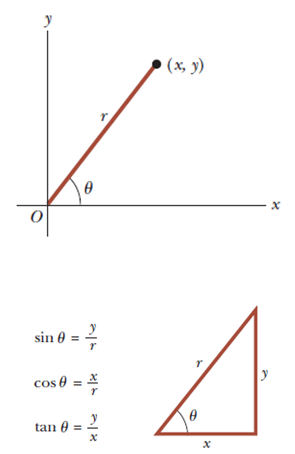
※ 평면극좌표의 요소
① r: 직각 좌표의 원점 (0, 0)으로부터 한 점의 위치 (x, y)까지의 거리
② θ: 원점에서 주어진 점까지 그은 선분과 고정된 x-축(x-axis; x-) 사이의 각도
- 고정된 x-은 +x축을 의미한다.
- θ의 각도는 시계반대방향으로 측정(measured counterclockwise)한다.
[Fig 2]는 평면극좌표로부터 직각좌표를 얻는 방법이다.

벡터양과 스칼라양 Vector Quantities and Scalar Quantities
스칼라양(scalar quantity): 온도, 질량, 부피, 속력, 시간 등 방향성이 존재하지 않는 한 개의 숫자로 표현할 수 있는 물리량
- 스칼라양은 양 또는 음의 부호를 가질 수 있다.
- 스칼라양의 계산은 일반적인 산술 규칙을 따른다. (The rules of ordinary arithmetic are used to manipulate.)
벡터양(vector quantity): 변위, 속도, 힘 등 방향성이 존재하는 두 개의 숫자로 표현할 수 있는 물리량
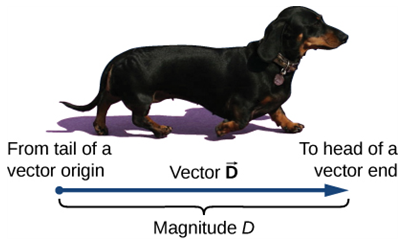
물리학에서 벡터 또는 벡터양은 화살표로 표현된다.
① 방향: 벡터 화살의 방향
② 크기: 벡터 화살의 길이
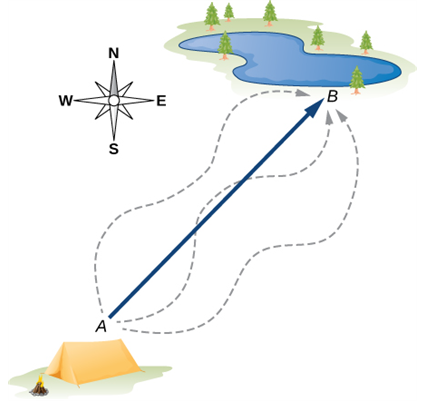
변위벡터(displacement vector): [Fig 4]처럼 단순히 입자의 시작점과 끝점을 이은 직선경로
※ 벡터의 표현

벡터의 크기는 항상 양수(always a positive number)이다.
벡터의 성질 Properties of Vectors
벡터의 동등성 Equality of Two Vectors
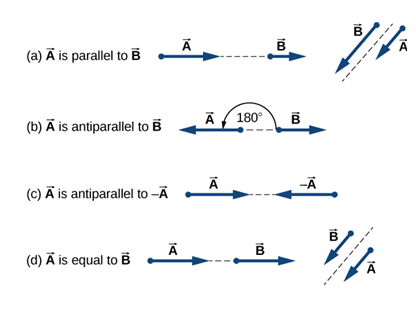
두 벡터 A, B의 동등성은 두 벡터의 크기 A, B가 서로 같고, 평행선을 따라 같은 방향을 가리킬 때[Fig 5]를 의미한다.
- 평행(parallel)
- 반평행(anti-parallel)
- 동등(equal)
equal한 벡터는 좌표계에서 평행이동이 가능하다.
벡터의 덧셈 Adding Vectors
합 벡터(resultant)
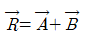
- 벡터 A의 꼬리에서 벡터 B의 머리까지 연결한 벡터
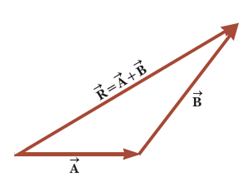
- 머리-꼬리법(head to tail method): 처음으로 더하려는 벡터의 꼬리에서 마지막 벡터의 머리 부분까지 연결한 벡터가 기하학적 resultant이다.
- 두 벡터를 더할 때 순서는 무관하다. (The sum is independent of the order.)
※ 벡터의 덧셈법칙
① 벡터 덧셈은 교환법칙이 성립한다.
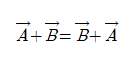
② 벡터 덧셈은 결합법칙이 성립한다.
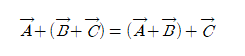
벡터를 더할 땐 반드시 같은 물리량을 가져야 한다.
음의 벡터 Negative of a Vector
음의 벡터: 벡터 A에 어떤 벡터를 더하여 그 합이 0이 되게 하는 벡터
- 벡터 A의 음의 벡터는 (-)벡터 A가 된다.
- 음의 벡터 A는 벡터 A와 크기는 같지만 서로 반대방향을 갖는다.
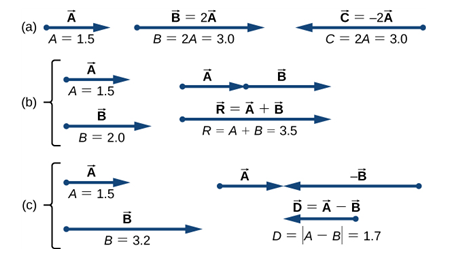
벡터의 뺄셈 Subtracting Vectors
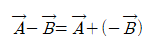
- 벡터 A 빼기 벡터 B는 벡터 A에 음의 벡터 B를 더한 값과 같다.
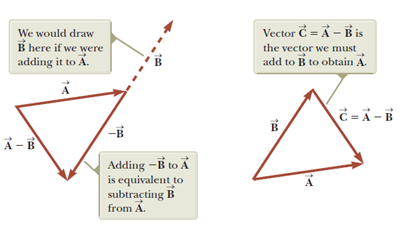
[1] 음의 벡터 B는 벡터 B와 크기는 같으나 정반대 방향을 갖는다.
[2] 벡터 빼기는 ‘음의 벡터를 더하는 것’과 같다.
[3] 벡터 빼기는 (1)음의 벡터 B를 벡터 A의 머리에 우선 이는 다음, (2)벡터 A의 꼬리에서 음의 벡터 B의 머리까지 연결한 벡터를 찾으면 된다.
스칼라양 곱하기 Multiplying a Vector by a Scalar
벡터 A에 스칼라양 m을 곱하면 그 곱은 벡터 A와 방향은 같으면서 크기가 mA인 ‘벡터’가 된다.
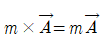
벡터 A에 음의 스칼라양 –m을 곱하면 벡터 A와 방향이 반대인, 크기 |-m|A인 벡터가 나온다. 벡터의 크기는 항상(always) 양수이기 때문에 음의 스칼라양에 절댓값을 취한 것에 유의한다!
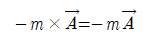
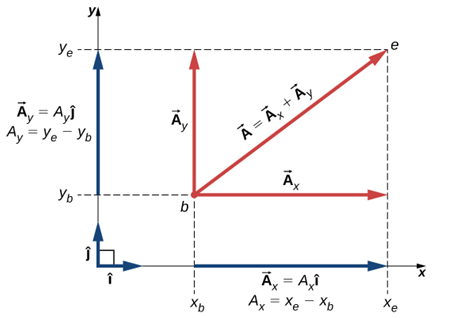
벡터의 성분과 단위 벡터 Components of a Vector and Unit Vectors
성분 벡터(component vectors, components): 어떤 벡터의 각 좌표축에 대한 사영(projection)
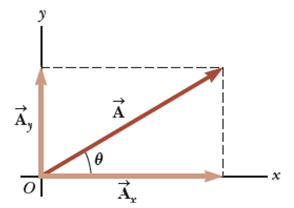
- 각 좌표축에 대한 성분벡터는 또한 직각성분(rectangular components)이라고도 불린다.
- [Fig 9]의 벡터는 +x-과 θ의 각을 이루고 있는데, 각 좌표축에 대해 두 개의 projection을 가지고 있다.
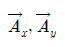
두 component vector는 [Fig 9]의 벡터와 다음 관계식을 만족한다.
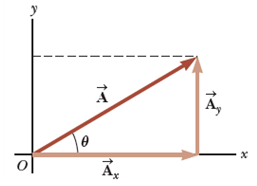
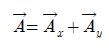
[Fig 10]에서 원(原)vector와 이것의 component vector는 직각삼각형을 이룬다.
- 성분벡터의 크기는 성분(component)이다.
- component는 스칼라양이다.
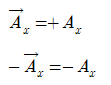
① 성분벡터의 방향이 +x-을 가리키면 component는 양수이다.
② 성분벡터의 방향이 –x-을 가리키면 component는 음수이다.
③ 성분벡터의 방향이 +y-(평면상의 y축의 위쪽방향)을 가리키면 component는 양수이다.
④ 성분벡터의 방향이 –y-(평면상의 y축의 아래쪽방향)을 가리키면 component는 음수이다.
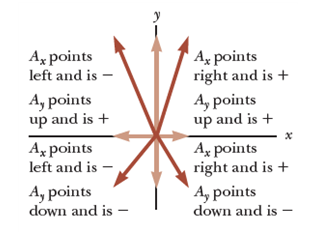
[Fig 10]은 직각삼각형을 이루며, 원벡터와 성분을 다음과 같이 정리할 수 있다.

성분의 부호는 각도 θ에 따라 결정된다.
예를 들어 경사면을 따라 미끄러지는 물체는 x축을 경사면으로 y축을 경사면에 수직하게 정하는 것이 좋다.
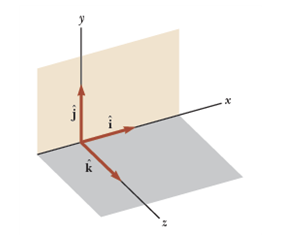
단위 벡터 Unit Vector
단위벡터(unit vector): 차원이 없고 크기는 1인, 방향을 표시하기 위한 벡터
- hat i, j, k는 각각 양(+)의 x, y, z-을 나타낸다[Fig 13].
- 벡터의 크기
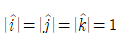
단위벡터를 이용해 성분벡터와 원벡터를 다음과 같이 표현할 수 있다.
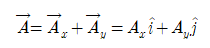

※ 2차원 벡터 덧셈
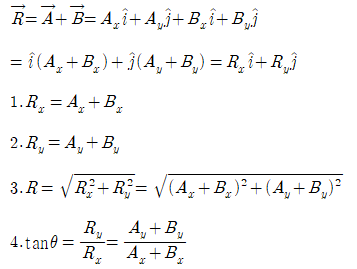
'고급물리학 > 고전역학' 카테고리의 다른 글
| 【2022 물리학 | 고전역학】 일차원 상에서의 운동 2 | 등가속도 운동 공식 유도 (0) | 2022.01.01 |
|---|---|
| 【2022 물리학 | 고전역학】 일차원 상에서의 운동 1 (0) | 2022.01.01 |
| [Mechanics] 유체저항력 | Resistive Forces (0) | 2020.05.17 |
| [Mechanics] 질량 시스템: 수직항력, 마찰력 | Normal Forces and Frictional Forces of Mass Systems (0) | 2020.05.17 |
| [Mechanics] 질량 시스템: 줄 연결, 접촉물체 | Types of Mass Systems (0) | 2020.05.17 |