
두 물체 사이의 중력이란, 물체의 각각의 중력질량의 곱에 비례하고,
두 물체 사이의 거리의 제곱에 반비례하는 잡아당기는 힘이다.
만유인력의 법칙의 현대적 해석
만유인력의 법칙의 현대적 해석과 달리, 원래 『프린키피아』에서는 만유인력을 '행성이 원뿔곡선의 궤도를 가지려면 태양이 행성에 작용한 구심력의 거리의 제곱에 반비례해야함'을 설명, 기하학적으로 증명했다. 또한 구심력이 거리의 제곱에 반비례하면, 행성 궤도는 원뿔곡선을 가짐을 보였다.
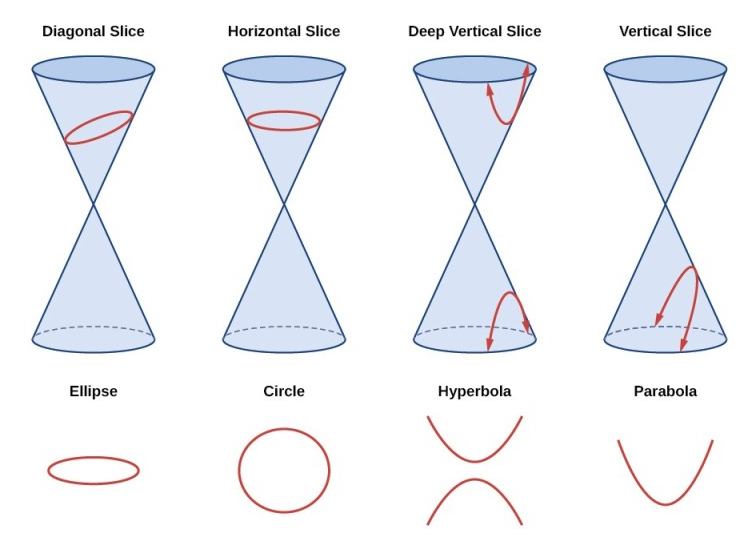
- 원뿔(cone)이란 [그림 1]처럼 '콘' 모양을 한 밑면이 원인 뿔이다. 이것을 어떻게 자르느냐에 따라 절단면이 만드는 곡선의 형태가 결정되는 데, 이들을 원뿔곡선(conic curve)이라 한다.
- conic curve의 종류
ⓐ 타원(ellipse)
ⓑ 원(circle)
ⓒ 쌍곡선(hyperbola)
ⓓ 포물선(parabola)
뉴턴 이전의 발견
Newton의 만유인력에 관한 설명에는 아래와 같은 선대 자연철학자들의 노력이 바탕이 되었다.

요하네스 케플러(Johannes Kepler, 1571-1630, 신성로마제국)의 행성운동 삼법칙
① 타원궤도의 법칙: 행성은 태양을 한 초점에 두고 타원 궤도로 공전한다.
② 면적속도일정의 법칙: 행성과 태양을 연결한 가상의 선이 단위시간 동안 휩쓴 면적은 항상 일정하다.
③ 조화의 법칙: 행성의 공전주기의 제곱은 행성궤도의 장반경의 세제곱에 비례한다.
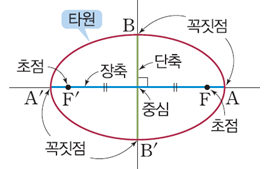
Kepler는 고대 그리스의 수학자 아폴로니오스(페르게의 아폴로니오스, Apollonius of Perga, B.C. 240- B.C. 190)의 원뿔곡선 내용을 이미 잘 이해하고 있었고, 이를 활용하여, 행성운동의 세 가지 법칙을 정립하였다,
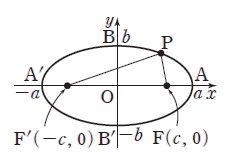
Apollonius의 타원이란, 두 점 F, F'에서 떨어진 거리의 합이 일정한 점들의 자취[그림 2]이며, [그림 3]과 같이 점 P와 초점 F, F'의 좌표를 정의했을 때, 타원은 다음 식을 만족한다.

- [그림 3]의 a는 장반경, b는 단반경이라고 불린다.

갈릴레오 갈릴레이(Galileo Galilei, 1564-1642, 중세 이탈리아 토스카나 대공국)의 발견
갈릴레이의 두 가지 중요한 발견 또한 Newton의 만유인력 이론에 영향을 주었다.
① 관성의 법칙: 물체에 외부의 힘이 작용하지 않는다면 물체는 항상 원래의 운동상태를 유지한다.
② 낙체의 법칙: 자유낙하(free fall)하는 물체가 떨어지는 거리는 시간의 제곱에 비례한다.
뉴턴의 정리
뉴턴은 저서 프린키피아 제1권에 만유인력의 기하학적 증명을 위한 '공리 체계'를 다음과 같이 정리하였다.
정의(definition)
프린키피아의 시작은 물리량을 정의하는 데서 출발한다.
정의 1. 물질의 양(quantity of matter)이란 물질을 밀도 ρ와 부피 V의 곱으로 측정한 값이다.
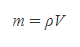
- 현대 물리학에서 물질의 양은 '질량'과 같다.
정의 2. 운동의 양(quantity of motion)이란, 운동의 속도 v와 물질의 양 m을 곱한 값이다.

- 뉴턴에게 운동의 양이란 현대물리학의 '운동량(momentum)'과 같다. 즉, 질량이 클수록 운동의 양이 커진다는 관념(concept)을 수식화하였다.
정의 3. 물질의 고유한 힘이란, 물체가 정지해있거나 등속 직선운동을 하는 상태를 유지하고 변화에 대해 저항하는 능력이다.
- 물질의 고유한 힘의 현대적 해석은 '관성'으로 풀이할 수 있다. Newton을 갈릴레이의 관성을 '물질이 내재한 고유한 힘'으로 간주했다.
- 물질의 관성(inertia)은 '물질이 최후로 가진 운동상태를 유지하려는 성질'이다.
정의 4. 외부의 힘(external force)에 의해 물체는 운동의 상태가 변한다. 정지 상태나 등속 직선운동을 하는 물체에 외부의 힘이 작용하면 이 운동 상태가 깨어진다.
- '내재된' 힘이었던 inertia의 대척점에 외력(external force)과 그 효과를 기술했다.
- 외부의 힘에 의해 운동의 상태가 깨어짐을 측정하기 위해서 Newton은 운동의 양이 변화하는 것으로 개념을 확장시켰다.
- 그냥 힘이 아닌 외부의(external) 힘을 강조한 것은 물체 내부의 힘은 물체의 운동의 양을 변화시키지 않음을 함의하기 위함이다.
이외에도 구심력 등의 물리량을 차례로 정의하고 있다.
공준(postulate)
Newton은 유클리드 『기하학원론』의 서술방식을 따랐고, 그의 postulate는 현재 '뉴턴의 운동 3법칙'으로 불린다.
운동 제1법칙: 모든 물체는 외부의 힘에 의해 변화가 생기지 않는 한 정지상태 또는 등속직선운동상태를 유지한다.
- Newton의 운동 제1법칙은 Galilei의 발견 및 [정의 3]과 매우 유사하다. 다만 외부의 힘과 운동의 관계를 조금 더 기술한 수준이다.
- 운동 제1법칙의 이름에 걸맞게 '모든 물체'라는 전제를 통해 우주의 어떤 물체에 대해서라도 내용이 항상 성립함을 알 수 있다.
운동 제2법칙: 운동의 변화는 외부에서 주어지는 힘(외력)의 크기에 비례하고 그 힘이 주어지는 직선방향으로 발생한다.
- 라틴어 원전을 직역한 제2법칙의 내용: "운동의 변화는 가해진 힘에 비례하고, 힘에 가해진 직선방향으로 일어난다."
- Newton이 생각한 운동의 변화란, 운동의 양이 변화하는 것으로, 힘 F ∝ 운동량의 변화량 Δp으로 요약할 수 있다.
- Newton은 이후 경험을 바탕으로 위의 비례식을 등식으로 만들기 위해, 힘에 의해 단위시간당 운동량의 변화량이 변한다라고 정리하였다.
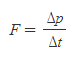

위의 식은 이후 스위스의 수학자 야코프 헤르만(Jacob Hermann, 1678-1733)과 스위스 바젤 출신의 수학자 레온하르트 오일러(Leonhard Euler, 1707-1783)가 다음과 같이 발전시킨다.
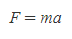
운동 제3법칙: 모든 작용(action)에는 언제나 반대방향으로의 크기가 같은 반작용(reaction)이 있다. 즉, 두 물체가 서로에게 가하는 작용은 크기가 같고 방향은 반대이다.
Newton의 따름정리(collorary)
세 가지 운동법칙을 기술한 이후 제2법칙의 따름정리(따름정리 1)로 다음 내용이 나온다.

따름정리 1: 어떤 물체에 두 가지 힘이 작용할 때, 두 힘을 평행사변형의 이웃한 변이라 생각하면 이것의 대각선 방향으로 힘이 작용하는 것과 같다.
- 따름정리 1을 통해 Newton은 힘의 효과가 '벡터적으로 나타남'을 최초로 표현했다.
(계속)
'고급물리학' 카테고리의 다른 글
| 【자연철학의 수학적 원리】 제2장. 타원궤도를 도는 물체의 만유인력 법칙의 기하학적 유도 <Part 1> (0) | 2022.01.30 |
|---|---|
| 【자연철학의 수학적 원리】 제1장. 뉴턴이 정리한 운동법칙 <Part 2> (0) | 2022.01.29 |
| 【과학고전 읽어보기】 자연철학의 수학원리 - 소개 (0) | 2022.01.25 |
| 반사와 굴절 (0) | 2021.12.11 |
| 가우스의 법칙 (0) | 2021.12.05 |