
천체가 타원의 궤도로 움직일 때, 타원의 초점을 향하는 구심력은 역제곱의 법칙을 따른다.
프린키피아 제1권, 제3장, 명제 11, 문제 6
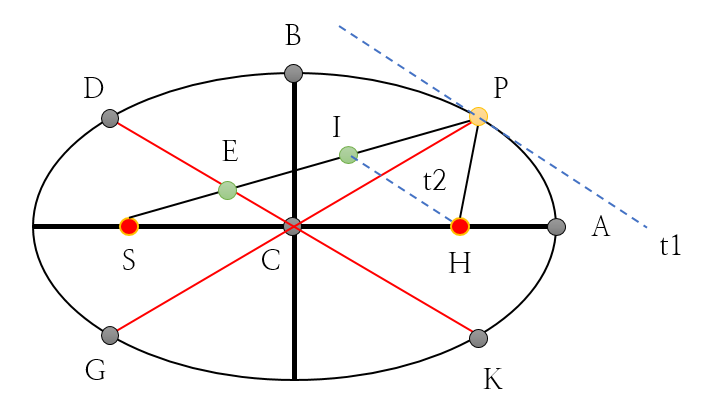
타원궤도를 도는 물체의 만유인력 법칙을 이야기하기 위해 먼저 [그림 1]의 선분 EP와 선분 AC가 서로 같은 길이를 가짐을 기하학적으로 증명할 수 있어야 한다.
선분 EP = 선분 AC
[1] [그림 1]의 조건
- 선분 PG와 선분 DK가 서로 켤레지름이다.
- 선분 AC는 타원의 장반경이고, 선분 BC는 타원의 단반경이다.
- 점 S와 점 H는 초점이다.
- 점 E는 선분 PS와 선분 DK가 만나는 교점이다.
- 선분 IH는 타원의 또 다른 초점에서 DK와 평행한 직선이다.
- 점 I는 선분 DK와 평행한 직선에 의해 선분 PS와 만나는 점이다.
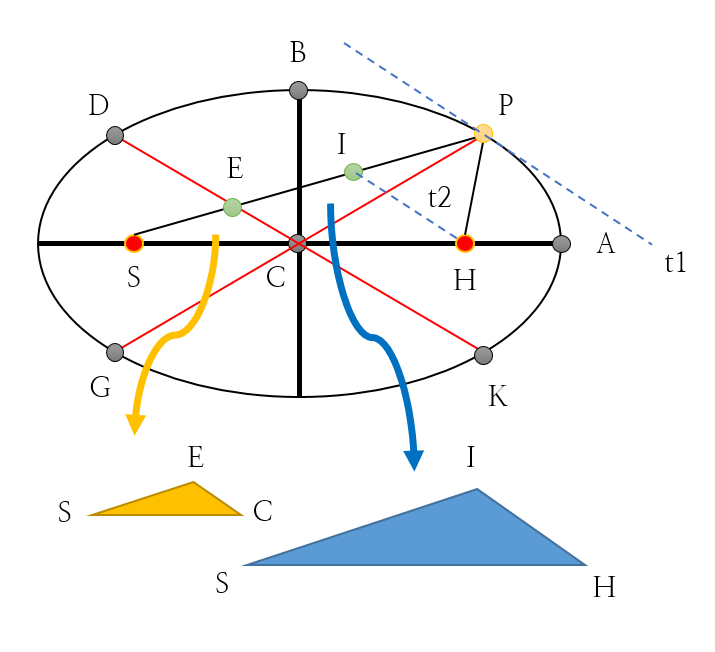
[2] 선분 CE와 선분 IH는 서로 평행하므로 삼각형 SHI와 삼각형 SCE는 서로 닮았다[그림 2].
[3] 타원의 중점으로부터 두 초점은 서로 거리가 같기 때문에(선분 CS=선분 CH), 선분 ES와 선분 EI의 길이는 서로 같다.
[4] 선분 EP의 길이
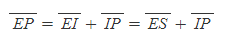
[5] [그림 1]의 접선 t1은 점 P에 그려진 것으로, 선분 DK가 켤레지름이기 때문에 이 접선과 평행한다.
[6] 또한 타원의 또 다른 초점 H에서 선분 DK와 평행한 직선을 그렸을 때, 다음을 만족한다.
- 선분 DK와 선분 IH는 서로 평행한다.
- 선분 CE와 선분 IH는 서로 평행한다.
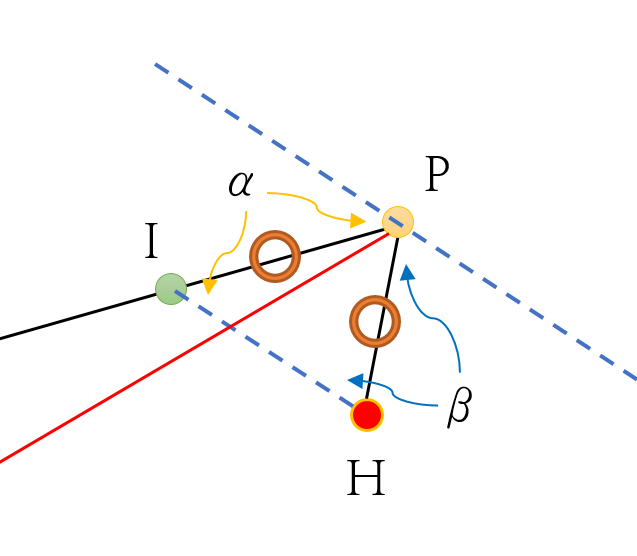
[7] 선분 IH와 접선 t1이 서로 평행하므로 두 개의 각 α, β는 쌍으로 각각 엇각으로 같다.
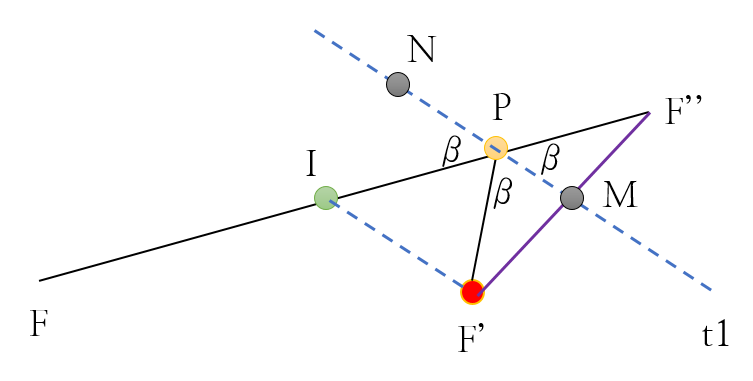
[8] 타원의 반사법칙
[그림 4]와 같이 두 초점 F, F'인 타원 위의 한 점 P에 대한 접선 t1을 그리고, F'에 대칭이동한 점 F''을 두면, 각 FPN과 각 F'PM이 서로 같다.
[9] [그림 3]의 두 개의 각은 [과정 8]의 타원의 반사법칙에 의해 두 각은 α=β의 관계식을 만족한다. 즉, 삼각형 PIH는 선분 PI와 선분 PH의 길이가 같은 이등변삼각형이다.
[10] 선분 EP=선분 AC의 증명

방멱 정리 Power of a Point Theorem
[그림 1]의 기하학적 모양을 수식화하기 위해 타원의 방멱 정리에 대해서 알아야 한다.
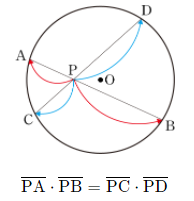
- 방멱: 어떤 한 점 P를 지나는 직선이 중심 O인 어떤 원 C와 만나는 점을 A, B라 했을 때, 두 선분의 곱 (선분 PA)×(선분 PB)
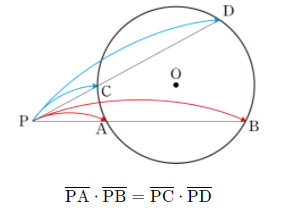
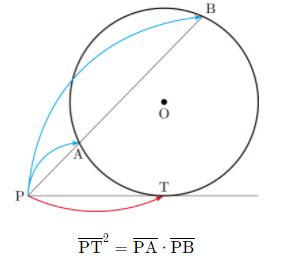
먼저 원의 방멱 정리는 (1)두 현(chord), (2) 두 할선, (3) 그리고 할선-접선에 대해 아래 세 개의 관계식을 만족한다.
원뿔곡선 1권 정리 38
Apollonius는 타원의 방멱 정리를 위해 자신이 정리한 『원뿔곡선』 1권의 정리 38을 활용한다.
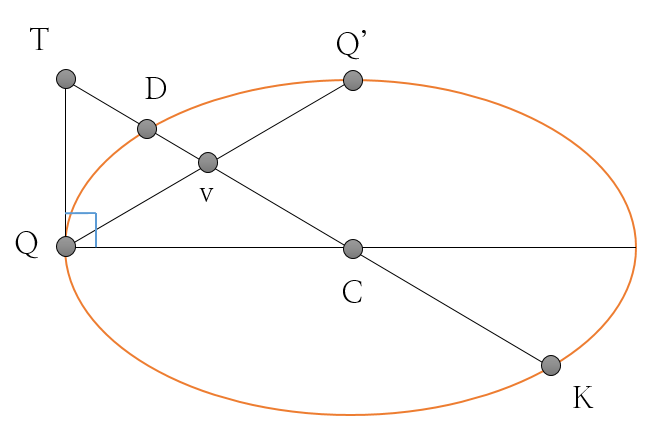
선분 DK가 타원의 지름이고 선분 QQ'가 점 D에서 접선과 나란한 현이라면, 선분 QQ'는 선분 DK에 의해 점 v에서 이등분 된다. 점 Q에서의 접선이 선분 DK를 연장한 직선과 점 T에서 만난다면,
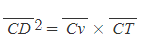
를 만족한다.
원뿔곡선 1권 정리 21: 타원의 방멱정리
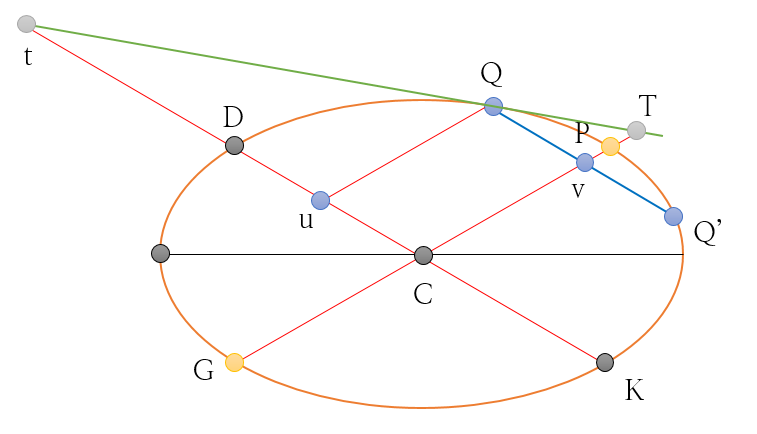
[그림 9]와 같이 (1)선분 PG와 선분 DK가 켤레지름이고, 선분 PG가 현 QQ'과 선분 DK를 각각 점 v와 점 C에서 이등분하면,
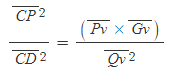
을 만족한다.
PROOF. 타원의 방멱 정리
[1] 조건
- 선분 PG와 선분 DK는 서로 켤레지름이다.
- 선분 Qv는 선분 DK와 나란하다.
- 선분 Qu: 선분 PG와 나란하고 점 Q를 지나는 선분, 선분 Qu와 선분 PG는 서로 평행한다.

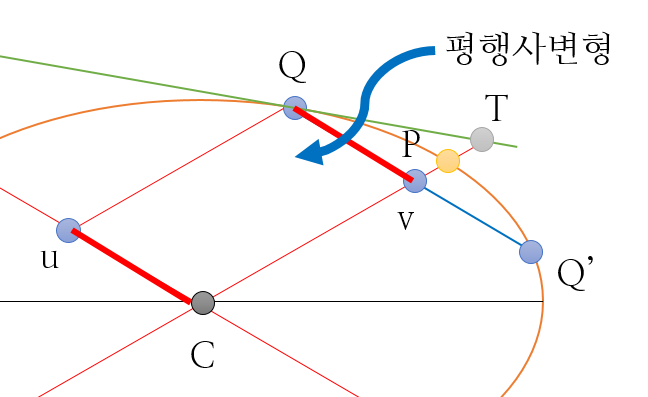
- 점 T: 점 Q에서 그은 접선 상에 선분 PG의 연장선과 만나는 점[그림 9]
- 점 t: 점 Q에서 그은 접선 상에 선분 DK의 연장선과 만나는 점[그림 9]
[2] Apollonius의 1권 정리 38에 의해 다음 식이 만족한다.
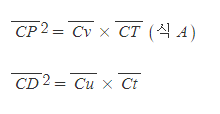
선분 CD의 제곱에 관한 식의 선분 Cu는 선분 Qv와 그 길이가 같으므로,
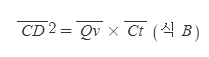
[3] [과정 2]의 식 A를 식 B로 나누면,
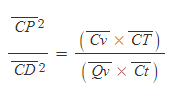
이다.
[4] [그림 9]의 삼각형 CtT와 삼각형 vQT는 (1)각 tCT와 각 QvT는 동위각이고 (2)각 T는 서로 공통이므로. 닮은꼴이다. 둘은 닮은꼴 삼각형이므로 다음과 같은 비례식 및 등식을 세울 수 있다.
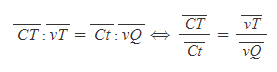
[5] [과정 4]의 결과를 [과정 3]의 식에 대입하면,
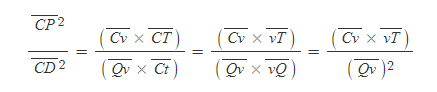
[6] 선분 vT는 선분 CT-선분 Cv와 같다.
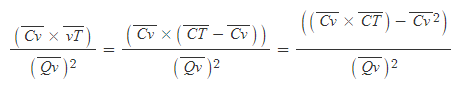
[7] [과정 2]의 식 A를 이용해 [과정 6]의 식을 다음과 같이 변환, 인수분해할 수 있다.
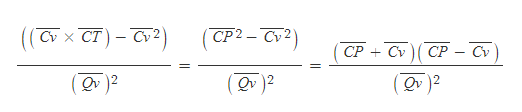
[8] [그림 9]에 따르면,
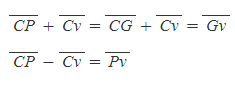
이다.
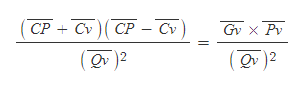
[9] 따라서 타원의 방멱정리를 다음과 같이 정리할 수 있다.
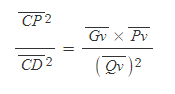
'고급물리학' 카테고리의 다른 글
| 【자연철학의 수학적 원리】 제3장. 케플러의 제3법칙 증명 - 원으로 도는 행성 (0) | 2022.02.01 |
|---|---|
| 【자연철학의 수학적 원리】 제2장. 타원궤도를 도는 물체의 만유인력 법칙의 기하학적 유도 <Part 2> (0) | 2022.01.30 |
| 【자연철학의 수학적 원리】 제1장. 뉴턴이 정리한 운동법칙 <Part 2> (0) | 2022.01.29 |
| 【자연철학의 수학적 원리】 제1장. 뉴턴이 정리한 운동법칙 <Part 1> (0) | 2022.01.29 |
| 【과학고전 읽어보기】 자연철학의 수학원리 - 소개 (0) | 2022.01.25 |