
부터 타원의 방멱정리까지 만유인력 법칙의 기하학적 증명을 위한 다양한 배경지식을 학습했다.
- 구심력 F
- 수직지름 L
- 선분 EP=선분 AC (+타원의 반사법칙)
- 타원의 방멱정리 (+원뿔곡선 1권 정리 38)
타원에 외접하는 평행사변형의 넓이는 모두 같다: 『원뿔곡선』 정리 136
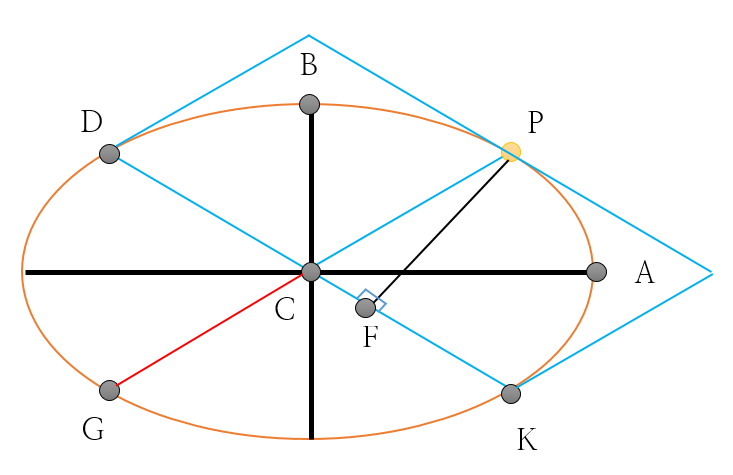
[그림 1]과 같이 주어진 타원에서 선분 PG와 선분 DK는 서로 켤레지름이고, 점 P에서 선분 DK로 내린 수선의 발을 F라 하면 다음 식을 만족한다.
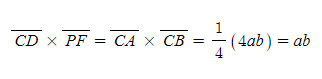
천체가 타원궤도로 움직이면 타원의 초점을 향해
거리의 제곱에 반비례하는 구심력이 작용한다.
프린키피아 제1권, 제3장, 명제 11, 문제 6
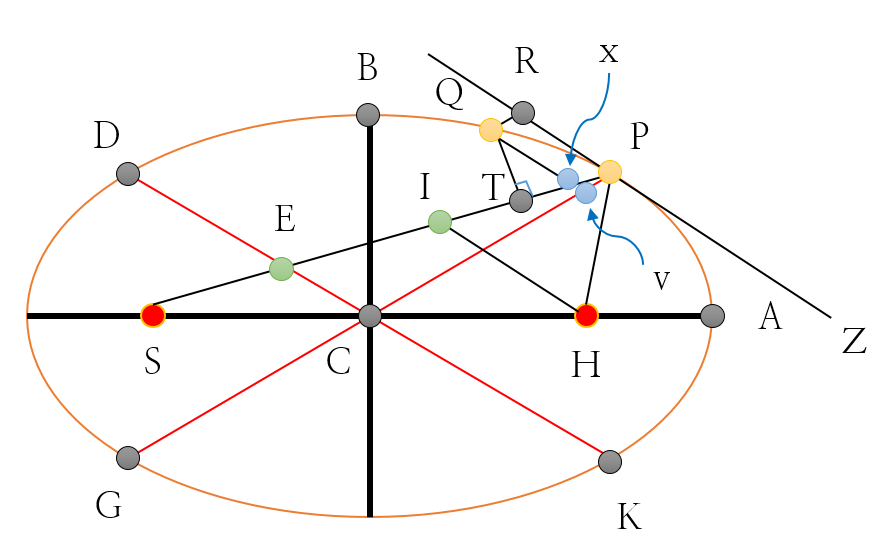

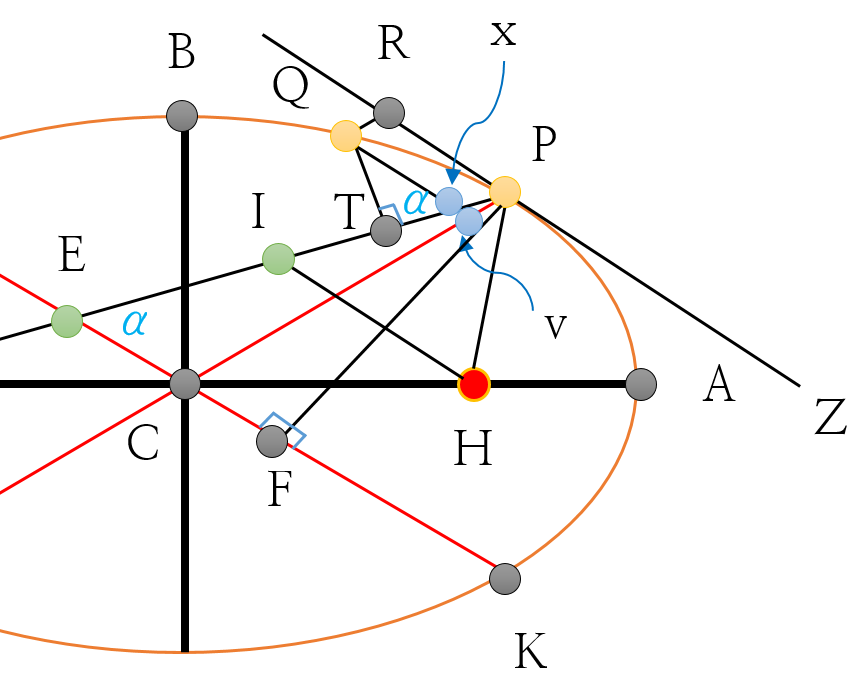
현 스웨덴 남부의 스코네 출신의 덴마크인 천문학자 티코 브라헤(Tycho O. Brahe, 1546-1601)는 자신의 화성궤도 연구 데이터를 Kepler에게 물려주었고, Kepler는 그 자료를 8년 동안 계산하여 화성의 궤도가 '타원'임을 입증했다. Newton 또한 이러한 관측(실측) 데이터를 받아들여, 타원궤도를 도는 물체의 만유인력 법칙(역제곱 법칙)을 유도하기 위해 [그림 2]의 S 자리에 태양이 고정되어 있고, 행성(화성)이 점 P점에서 출발하여 점 Q로 이동한다고 설정했다.
[1] 태양이 구심력을 작용할 때 행성의 위치는 점 Q로 이동한다. 그러나 구심력이 없다면 행성의 위치는 점 R로 이동한다.
[2] 점 Q를 지나고 선분 PR에 평행한 직선을 그릴 때, 그 직선이 선분 SP와 만나는 점을 x라 한다. 한편 점 Q를 지나고 선분 PR에 평행한 직선을 그릴 때, 그 직선이 선분 CP와 만나는 점을 v라 한다.
- 사각형 QRPx는 평행사변형이다.
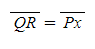
[3] 삼각형 PEC와 삼각형 Pxv는 닮음이다.
- 선분 EC와 선분 xv는 평행이다.
- 각 EPC는 공통이다.
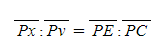
[4] 선분 Px는 선분 QR이고, 선분 EP는 선분 AC와 같다.
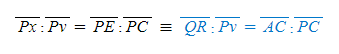
선분 QR, 선분 Pv의 좌변항에 수직지름 L을 곱해줘도 비례식은 여전히 유효하다. 왜냐하면 L=2b/a로 항상 일정한 값이고 비례식을 등식으로 만들 때 L이 양변에 곱해지기 때문이다.
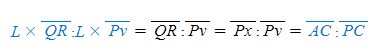
[5] 타원의 방멱정리를 비례식으로 쓰면 다음과 같다.
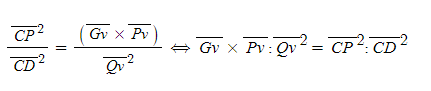
[6] 점 Q에서 선분 EP에 내린 수선의 발을 T, 점 P에서 선분 DK에 내린 수선의 발을 F라고 하면, 삼각형 TQx와 삼각형 FPE는 닮음이다.
- 각 QTx = 각 PFK = 각 PFE
- 선분 Qx와 선분 EF는 평행한다.
- 위의 두 조건에 의해 각 QxT = 각 FEP(엇각)을 만족한다.
[7] 삼각형의 닮은비 법칙
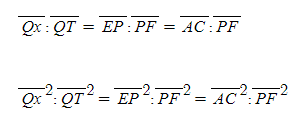
비례식에 대해 모든 항을 제곱해도 그 비례식은 성립한다.
[8] 행성이 P에서 Q로 이동할 때 그 시간이 극히 짧다면(dt) 선분 Qv는 선분 Qx로 근사할 수 있다.
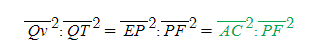
[9] Apollonius의 『원뿔곡선』에 나오는 정리 136의 식을 비례식으로 만들면 다음과 같다.
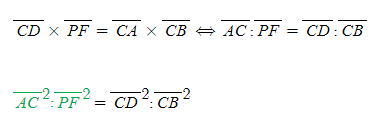
[10] [과정 8]의 제곱비례식과 [과정 9]의 제곱비례식을 조합하여, 다음 새로운 비례식을 유도한다.
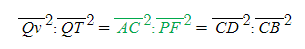
[11] 여러 비례식의 분수화
- (좌변)=(우변)의 비례식 꼴인 A:B=C:D의 식은 다음과 같이 분수식으로 만들 수 있다.
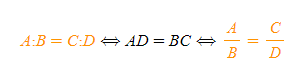
- [그림 2]의 중요한 비례식은 다음과 같다.
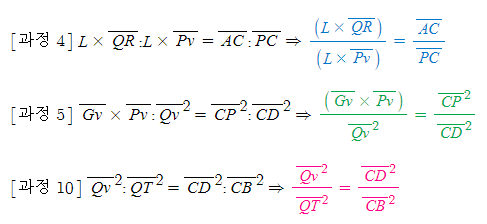
- 위의 분수식은 [그림 2]의 동일한 조건에서 나온 식들로 좌변 전체와 우변 전체를 아래와 같이 곱해 둘이 서로 같다고 할 수 있다.
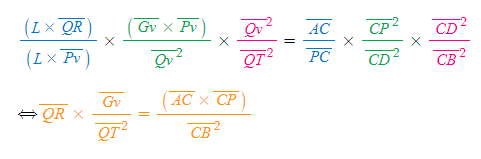
- 수직지름 L은,
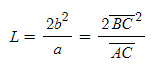
인데, 위의 식을 L에 대해 치환하면,
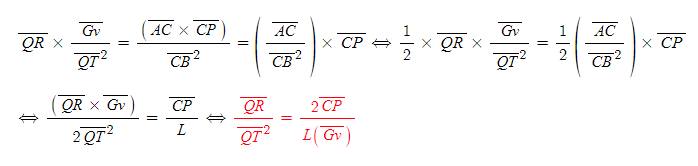
으로 계산가능하고 선분 QR/선분 QT^2으로 구심력 F의 비례식에 등장한 항으로 내용을 총정리할 수 있다.
▼ 구심력의 비례식 다시 확인하기

[12] 행성이 P에서 Q로 이동할 때 운동하는 시간이 극히 짧다면(dt),
1. Q→P이고
2. 선분 Gv→선분 GP로 수렴한다.
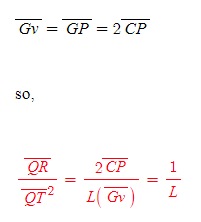
구심력의 공식 정리
명제 6, 정리 5, 따름정리 1에 따르면 구심력 F는 다음과 같은 등식을 만족한다.
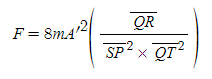
그리고 이제 우리는 선분 QR/선분 QT^2의 정확한 값을 안다.
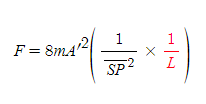
주어진 타원궤도에 A'은 단위시간에 훑고 지나간 면적을 의미하고, 면적속도일정의 법칙에 의해 항상 일정한 값을 갖는다. m은 행성의 질량이므로 당연히 상수로 취급되고, L 또한 타원궤도의 수직지름으로 2b^2/a라는 항상 일정한 값을 가지므로, 구심력 F는 결국 태양(S)과 행성(P)간의 직선거리인 선분 SP의 제곱에 의해서만 그 값이 결정됨이 증명되었다.
이것이 바로 역제곱 법칙의 기하학적 증명이다.
'고급물리학' 카테고리의 다른 글
| 【자연철학의 수학적 원리】 제3장. 케플러의 제3법칙 증명 - 타원으로 도는 행성 [完] (0) | 2022.02.02 |
|---|---|
| 【자연철학의 수학적 원리】 제3장. 케플러의 제3법칙 증명 - 원으로 도는 행성 (0) | 2022.02.01 |
| 【자연철학의 수학적 원리】 제2장. 타원궤도를 도는 물체의 만유인력 법칙의 기하학적 유도 <Part 1> (0) | 2022.01.30 |
| 【자연철학의 수학적 원리】 제1장. 뉴턴이 정리한 운동법칙 <Part 2> (0) | 2022.01.29 |
| 【자연철학의 수학적 원리】 제1장. 뉴턴이 정리한 운동법칙 <Part 1> (0) | 2022.01.29 |