
힘의 중심이 고정되어 있고, 어떤 물체가 둘레를 공전할 때
그 중심과 물체를 잇는 반경을 그리는 면적은
일정한 평면을 유지하며 시간에 비례한다.
『프린키피아』, 제1권, 제2장, 명제 1, 정리 1
프린키피아, 제1권, 제2장의 명제 1, 정리 1은 Kepler의 행성운동에 관한 제2법칙(면적속도일정의 법칙)을 다음과 같이 재해석한다.
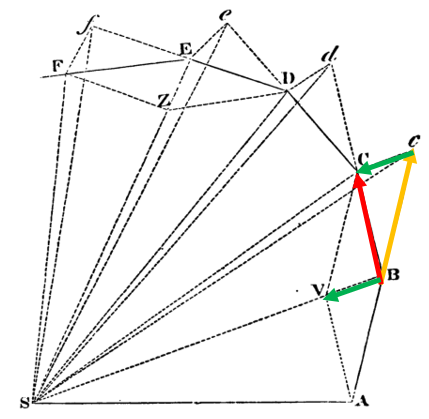
[그림 1]은 일정한 시간 dt 동안 행성이 지점 A에서 B, C, D, E, F...로 운동하는 것을 도식화한 그림인데, 점 S의 태양에 의해 행성은 구심력을 받고 있다.
만약 [그림 1]의 행성에 외력(external force)이 없다면, Newton의 운동 제1법칙에 따라 행성은 등속 직선운동을 할 것이다.
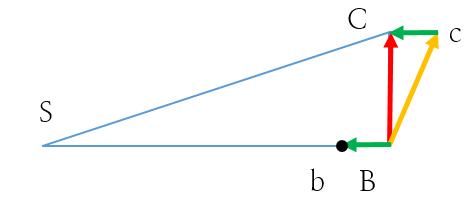
따라서 [그림 2]처럼 행성이 만약 점 B에 있다면 점 c로 이동했을 것이다. 그러나 S에 위치한 태양에 의해 구심력을 받아 점 B의 행성은 B→C로 이동하게 된다.
- 태양에 의한 중력에 의해 행성은 c에서 C로 '떨어지는 모양'을 한다.
구심력에 의해 행성은 가속을 받아 태양쪽으로 선분 cC만큼 떨어지고 이는 평행선 선분 bB과 그 크기가 같다.
Newton의 따름 정리 활용
행성이 B에서 C로 움직일 때 평행사변형 bBcC가 만들어지고 Newton의 따름 정리 1을 활용해 이를 벡터적으로 해석하면,
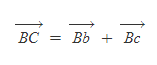
라 풀어쓸 수 있다.
ⓐ 선분 bB와 선분 cC는 서로 평행한다.
ⓑ 선분 SB와 선분 cC는 서로 평행한다.
ⓒ 삼각형 SBC와 삼각형 SBc는 밑변이 선분 SB로 공통이다.
두 삼각형의 밑변이 공통이고 ⓐ와 ⓑ 조건을 만족하기 때문에 삼각형 SBC와 삼각형 SBc의 높이가 같을 것이고, 따라서 두 삼각형의 면적 또한 같다. ⇒ 미소 시간 dt가 흘러 점 C에서 점 D로 움직일 때도 같은 원리로 삼각형의 면적은 항상 같고, 이를 통해 '단위 시간 동안 행성의 반지름이 훑고 간 면적이 같음을 기하학적으로 증명할 수 있다.
구심력에 관하여
프린키피아 명제 6, 정리 5, 따름정리 1에는 다음과 같은 내용이 나온다.

어떤 천체가 곡선 APQ를 그리며 중심 S의 둘레를 돌 때, 선분 ZPR은 점 P에서 이 곡선에 접하는 접선이다. 곡선 위의 다른 점 Q에서 선분 QR와 선분 SP가 평행이 되도록 점 R을 설정하고, 선분 QR을 그린다. 점 Q에서 선분 SP에 내린 수선의 발을 T라고 할 때, 점 S에서 점 P에 있는 행성에 작용한 구심력 F는,
로 비례한다.
PROOF. 명제 6, 정리 5, 따름정리 1
[그림 3]의 초기 조건에서 태양은 S, 행성은 P에 있다.
[1] [그림 3]의 점 P에 행성이 아주 짧은 시간 dt 동안 점 Q로 이동한다.
- 구심력이 없다면 점 R로 이동하는데, 이때 거리는 선분 PR=(행성의 속력)×dt로 계산할 수 있다.
[2] 점 Q로 행성이 이동하는 이유는 '구심력' 때문이고, 이는 행성의 가속도 a를 야기한다.
① 선분 QR만큼 행성은 태양을 향해 '떨어진다'. ⇒ Newton의 운동 제2법칙 적용
② 떨어지는 물체는 Galilei의 낙체의 법칙을 적용할 수 있다.
갈릴레이의 낙체의 법칙은,
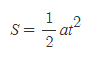
으로 적을 수 있다.
③ Galilei의 낙체의 법칙의 가속도 a에 운동 제2법칙 a=F/m를 대입한다.
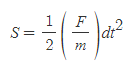
- 여기서 S는 선분 QR이라 할 수 있다.
[3] dt동안 선분 SP가 훑고 지나간 면적은 SPQ로 삼각형 면적으로 근사가능하다. dt는 매우 짧은 시간이기 때문에, 밑변 SP, 높이 QT의 삼각형 넓이(A)를 호의 면적과 같다고 둔다.
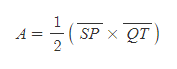
[4] Kepler의 면적속도일정의 법칙에 따라 선분 SP가 단위시간에 훑고 지나간 면적을 A'라고 했을 때,
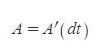
이다.
[5] [과정 3]과 [과정 4]의 A는 서로 등식으로,
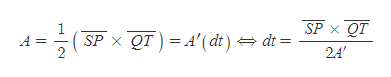
로 dt를 정리할 수 있다.
[6] [과정 2]의 낙체의 법칙의 dt와 [과정 5]의 dt는 서로 등식이다.
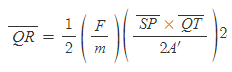
[7] [과정 6]의 식을 구심력 F에 대해 정리한다.
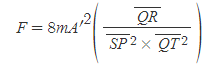
타원의 수직지름
겹세로축(double ordinate): 타원의 장축에 수직한 현
세로축(ordinate): 겹세로축의 1/2, 수직반지름이라고도 불림
수직지름: 겹세로축 중 초점을 지나는 현
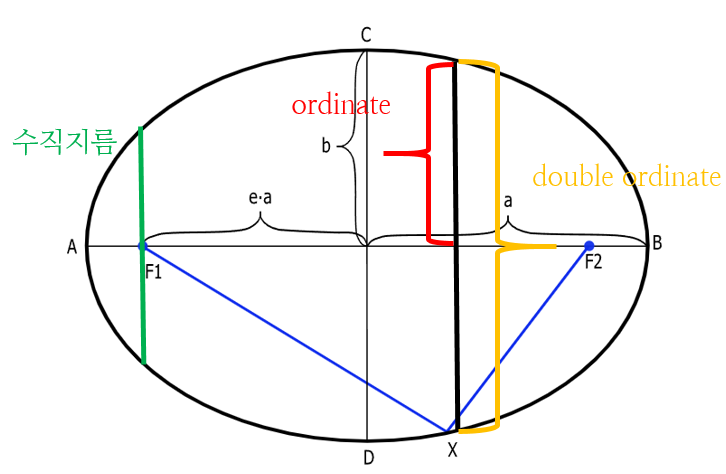
타원의 정의와 요소들을 이용해 수직지름의 식을 구해보자.
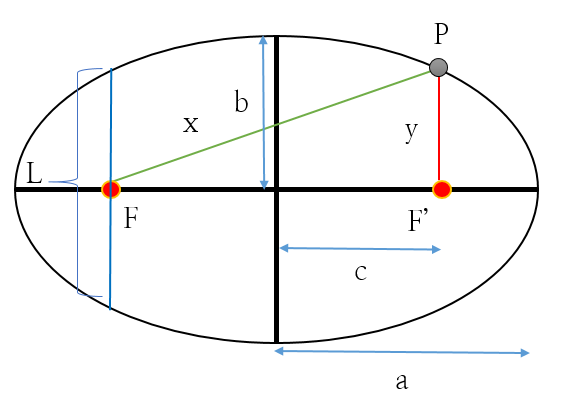
[1] [그림 5]와 같이 타원의 장반경은 a, 단반경은 b로 정의한다. 그리고 타원의 중점에서 초점까지의 거리는 c이다.
[2] Apollonius의 타원의 정의에 따라, [그림 5]의 타원은 다음 식을 만족한다.
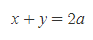
[3] 삼각형 FPF'는 직각삼각형이므로 피타고라스 정리를 이용할 수 있다.
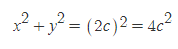
[4] [과정 2]와 [과정 3]의 내용을 연립하면 ordinate, 즉 수직반지름 y를 구할 수 있다.
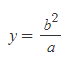
[5] 수직지름은 수직반지름의 2배이므로,
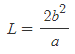
이다.
이제 구심력의 비례식과 타원의 수직지름이라는 배경지식을 활용해, 타원궤도일 때 만유인력의 법칙을 유도할 준비가 되었다.
'고급물리학' 카테고리의 다른 글
| 【자연철학의 수학적 원리】 제2장. 타원궤도를 도는 물체의 만유인력 법칙의 기하학적 유도 <Part 2> (0) | 2022.01.30 |
|---|---|
| 【자연철학의 수학적 원리】 제2장. 타원궤도를 도는 물체의 만유인력 법칙의 기하학적 유도 <Part 1> (0) | 2022.01.30 |
| 【자연철학의 수학적 원리】 제1장. 뉴턴이 정리한 운동법칙 <Part 1> (0) | 2022.01.29 |
| 【과학고전 읽어보기】 자연철학의 수학원리 - 소개 (0) | 2022.01.25 |
| 반사와 굴절 (0) | 2021.12.11 |