
Newton은 자신의 저서 『프린키피아』의 제1권, 제3장, 명제 11, 문제 6에서 '타원궤도로 움직이는 행성이 거리의 제곱에 반비례하는 구심력을 받음'을 기하학적으로 증명했다. 또한 학문적 스승인 Kepler가 발견한 행성 운동에 관한 제3법칙인 '조화의 법칙' 또한 같은 책 제1권, 제3장, 명제 15, 정리 7에서 이어 증명한다. Kepler의 조화의 법칙을 다시 설명하자면,
행성의 공전주기의 제곱은 행성궤도의 장반경의 세제곱에 비례한다.
로 요약할 수 있다.
Newton의 타원궤도 행성에 관한 조화의 법칙 증명을 쉽게 이해하기 위해 우선 행성이 원궤도를 돈다 가정한 뒤, 이를 수학적으로 증명해보자.
원의 이해
Euclid의 『기하원론』에서 원이란 다음과 같이 정의된다.
원이란, 주어진 한 점에서 거리가 같은 점들의 집합이다.
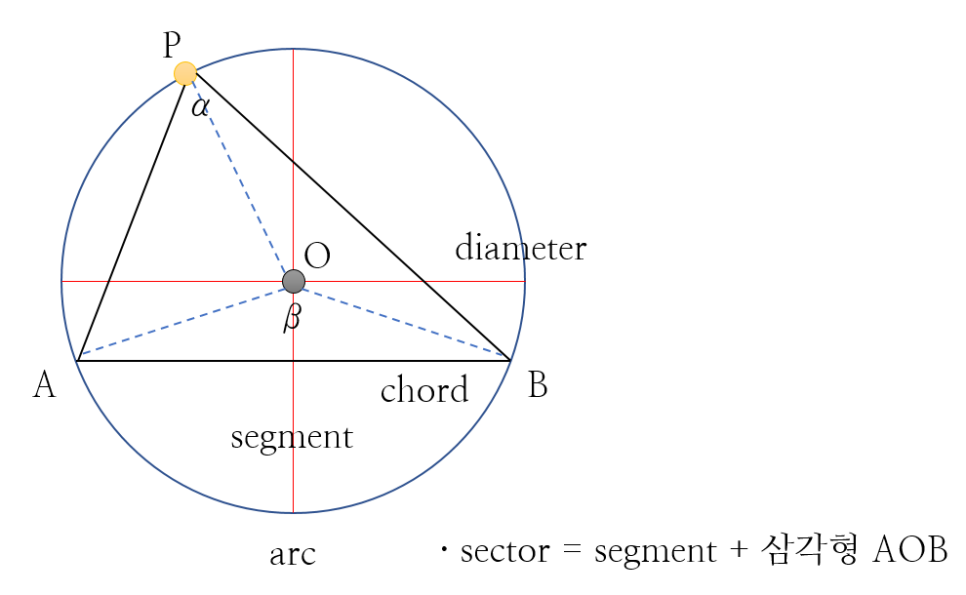
[그림 1]은 원에서 나타날 수 있는 다양한 요소로 다음과 같이 정의한다.
ⓐ 현(chord): 원 위의 두 점을 이은 선분 AB
ⓑ 지름(diameter): 원의 현 중 가장 긴 선분
ⓒ 호(arc): 현 AB를 두고 생기는 원의 일부분
- 현 AB를 기준으로 짧은 호는 (1)열호, 긴 호는 (2)우호라고 한다.
ⓓ 활꼴(segment): 현 AB와 호 AB로 경계지어진 영역(넓이)
ⓔ 부채꼴(sector): [그림 1]을 예로 들자면, 선분 OA, 선분 OB와 호 AB로 둘러싸인 모양으로 활꼴에 삼각형이 합쳐진 넓이
ⓕ 중심각: 호 AB에 해당하는 부채꼴의 중심에 생긴 각, [그림 1]의 경우 중심각은 β이다.
임의의 지점 P가 원에 지정되었다면, 선분 AB와 같이 새로운 두 선분을 그어 삼각형([그림 1]에서는 삼각형 APB)을 그릴 수 있는데, 호 AB에서 멀리 떨어진 P가 이루는 각([그림 1]에서는 α)을 원주각이라 한다.
원요소의 성질
1. 원주각과 중심각 사이에는 아래의 관계식이 성립한다.
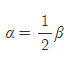
2. 원에서의 접선이란, 원 위의 임의의 한 점에서 그 점을 지나는 원의 반지름과 직각을 이루는 선을 뜻한다.
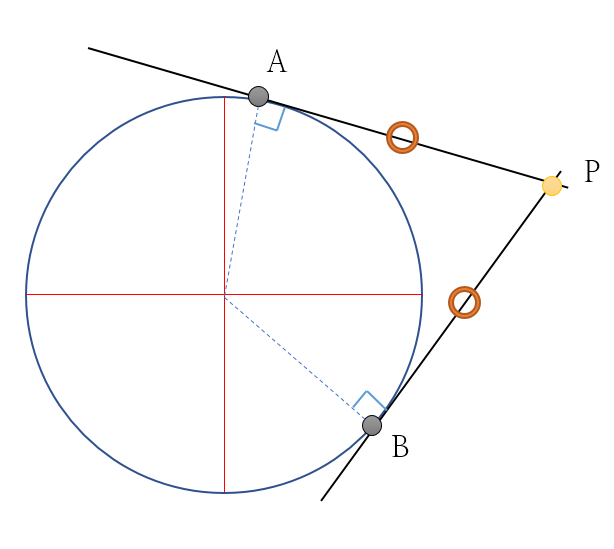
- 이 직각을 이루는 성질에 따라 '원 외부의 임의의 한 점에서 원에 접하는 두 직선을 그릴 때 접점까지의 거리가 모두 동일하다.'라는 결론을 얻을 수 있다. [그림 2]에 따르면,
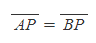
이다.
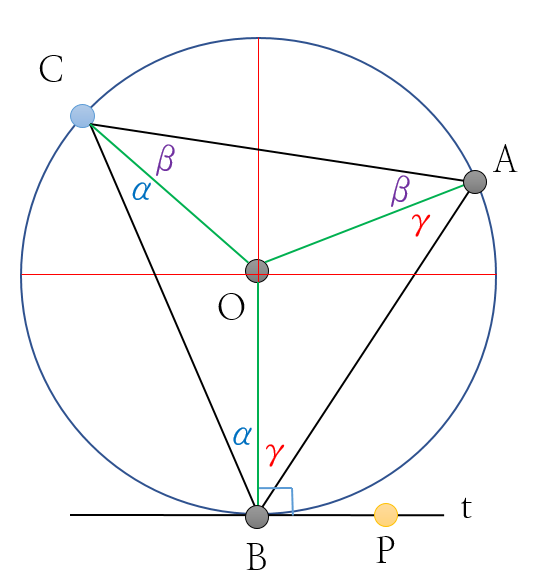
3. [그림 3]과 같이 임의의 점 P에 대해 원에 접선을 그었을 때, 접선(t)과 접점(B)을 포함한 현이 이루는 각도는 위와 같은 특성을 갖는다.
4. 원에서 현의 수직이등분선은 반드시 원의 중심을 지난다. 이 성질을 이용하여 원의 중심을 쉽게 찾을 수 있다.
5. 원의 방멱 정리(power of a point theorem)
원운동하는 행성의 조화의 법칙
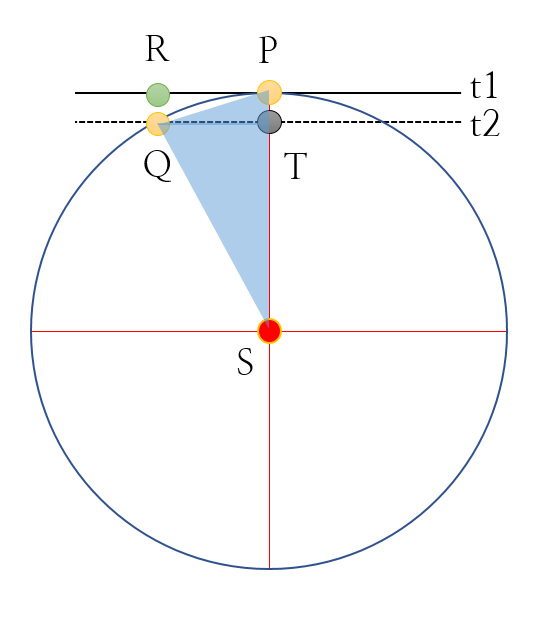
원운동을 하는 행성의 도식을 [그림 4]와 같이 요약할 수 있다.
- S: 태양
- P: 행성
- R, Q: 점 P의 행성이 태양 S가 없다면 구심력이 없어 등속 직선 운동을 하고 이에 미소 시간 dt동안 R로 이동할 것이다. 하지만 태양 S가 있다면 행성 P에 구심력이 작용해 행성은 미소 시간 dt동안 Q로 이동한다.
- 선분 QR: 행성은 태양을 향해 선분 QR만큼 '떨어진다고' 볼 수 있다.
- t1: 점 P의 접선
- t2: 행성이 점 Q로 이동했을 때 선분 t1과 평행한 직선
[1] 선분 QR은 Galilei의 낙체의 법칙에 따라,
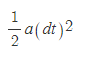
으로 적을 수 있으며, 가속도 a는 Euler가 수정한 Newton의 운동 제2법칙에 따라,
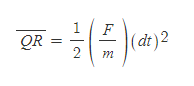
로 정리할 수 있다.
① F: 행성에 작용한 힘으로 구심력의 식을 대입할 수 있다.
② m: 행성의 질량
[2] 구심력 자리에 『프린키피아』 명제 6, 정리 5, 따름정리 1의 내용을 대입한다.
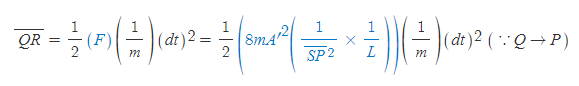
- 행성이 P에서 Q로 이동할 때 운동하는 시간이 극히 짧다고(dt) 앞서 가정했기 때문에, 수직지름 L이 포함된 식을 F에 쓸 수 있다.
- 타원의 수직지름 L은 원의 지름 2×(반지름 r)과 같다.
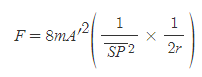
[3] 행성의 운동시간을 dt라 두었기 때문에 [그림 4]의 SPQ의 넓이를 삼각형의 넓이처럼 구할 수 있다.
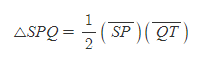
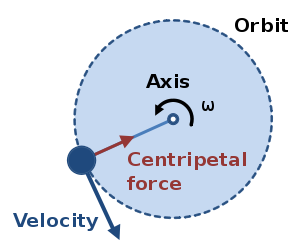
[4] Newton은 원운동(circular motion)을 다음과 같이 이해하였다.
- 어떤 물체의 원운동은 기본적으로 구심력에 의해 힘에 의한 운동이다.
- Kepler가 정리한 화성의 운동은 타원을 그리고 있으며, 그의 제2법칙(면적속도일정의 법칙)은 타원궤도의 위치에 따라 화성의 '속력'이 다름을 의미한다.
- 반면, 이 속력이 일정하다면 물체는 완전한 원을 그린다.
Newton은 이러한 추론으로 완전한 원을 그리는 물체의 '속력'은 항상 일정하다고 생각했고, 이러한 원운동을 현대물리학에서는 등속 원운동(uniform circular motion)라 한다.
[5] 태양과 행성을 잇는 직선 SP는 원을 그릴 때 일정한(constant) 면적속도 A'으로 이동한다. 시간이 t만큼 흐르면 직선 SP가 지나간 총 넓이는 A=A'×(t)로 계산할 수 있다. [그림 4]의 행성의 원운동은 그 시간을 매우 짧게 설정했기 때문에, A=A'(dt)로 구할 수 있는데, 여기서 A는 삼각형 SPQ와 같다.
- 극히 짧은 시간이기 때문에, 선분 SP가 P에서 Q로 이동할 때 그린 호 PQ를 선분 PQ처럼 생각할 수 있다.
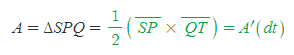
[6] [과정 2]의 구심력 식에서,
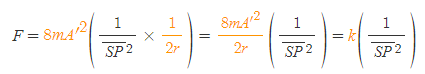
부분을 상수 k로 둘 수 있다.
[7] k를 다시 직선 SP가 지나간 면적속도 A'로 정리하면,
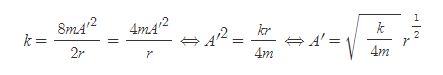
이다.
[8] 원운동을 하는 물체의 주기(period)는 물체의 거리(s)-시간(t)-속력(v)의 식을 변형한 아래의 식으로 표현할 수 있다.
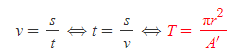
- 원운동의 주기란, 원운동을 하는 물체가 한 번 회전하는 데 걸린 시간으로 등속원운동에서 (1)속력 v인 입자는 한 주기 T 동안 원의 둘레(2πr)를 돌고 (2)면적속도 A'을 갖는 선분은 한 주기 T 동안 원의 면적(πr^2)을 지난다.
[9] [과정 8]의 주기 식에 [과정 7]의 A'을 대입한다.
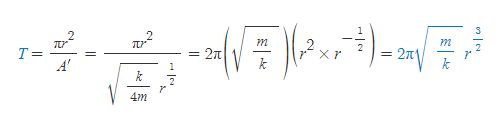
[10] [과정 9]의 T를 제곱하면,
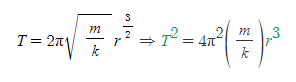
그러므로, 원궤도를 도는 물체는 Kepler의 제3법칙(조화의 법칙)을 아래와 같이 만족한다.
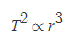
'고급물리학' 카테고리의 다른 글
| 【자연철학의 수학적 원리】 제3장. 케플러의 제3법칙 증명 - 타원으로 도는 행성 [完] (0) | 2022.02.02 |
|---|---|
| 【자연철학의 수학적 원리】 제2장. 타원궤도를 도는 물체의 만유인력 법칙의 기하학적 유도 <Part 2> (0) | 2022.01.30 |
| 【자연철학의 수학적 원리】 제2장. 타원궤도를 도는 물체의 만유인력 법칙의 기하학적 유도 <Part 1> (0) | 2022.01.30 |
| 【자연철학의 수학적 원리】 제1장. 뉴턴이 정리한 운동법칙 <Part 2> (0) | 2022.01.29 |
| 【자연철학의 수학적 원리】 제1장. 뉴턴이 정리한 운동법칙 <Part 1> (0) | 2022.01.29 |