Newton은 『프린키피아』 제1권, 제3장, 명제 15, 정리 7에서 Kepler의 제3법칙을 다음과 같이 정리, 증명했다.
행성이 태양을 타원궤도로 공전할 때, 중력은 둘 사이의 거리의 제곱에 반비례하며,
행성의 공전주기의 제곱은 그 행성의 공전 궤도의 장반경의 세제곱에 비례한다.
『프린키피아』 제1권, 제3장, 명제 15, 정리 7
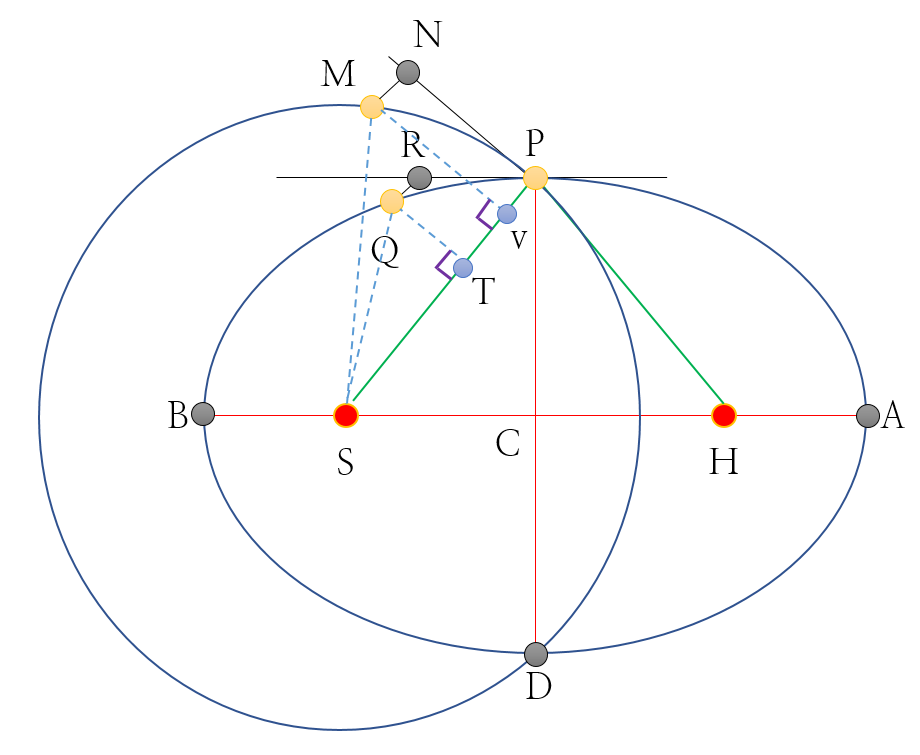
우선 [그림 1]의 내용을 다음과 같이 이해해야 한다.
ⓐ 태양은 점 S에 위치해있고, 행성은 점 P에 위치한다.
ⓑ 타원요소
- 선분 AB: 타원의 장축
- 선분 PD: 타원의 단축
- 선분 AC 또는 BC: 타원의 장반경, a ⇒ 선분 AB=2a
- 선분 PC 또는 CD: 타원의 단반경, b ⇒ 선분 PD=2b
- 타원의 수직지름은 L로 2b^2/a로 구한다.
- 타원의 정의
ⓒ 계산의 편의성을 위해 행성 P를 선분 PD의 단축 바로 위에 위치해있다고 하자.
- 선분 SP와 선분 HP의 길이는 서로 같다.
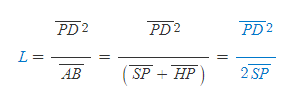
- 반지름: 선분 SP
이다.
[1] [그림 1]의 행성 P가 원궤도를 도는 경우
- 태양에 의한 구심력으로 행성 P는 원궤도에서 점 M으로 이동할 것이다. 중력이 없다면 점 N으로 이동하나 결국 중력에 의해 선분 MN만큼 떨어진다.
[2] [그림 1]의 행성 P가 타원궤도를 도는 경우
- 태양에 의한 구심력으로 행성 P는 타원궤도에서 점 Q로 이동할 것이다. 중력이 없다면 점 R로 이동하나 결국 중력에 의해 선분 QR만큼 떨어진다.
[3] 타원으로 도는 행성의 조화의 법칙 증명은 원의 반지름과 타원의 장반경의 크기가 같음을 규명하면 된다.
- 원의 반지름과 타원의 장반경의 크기가 같다면 원과 타원을 한 바퀴 도는 데 걸리는 시간 또한 같을 것이다. 천체가 궤도를 한 바퀴 돌아 처음 자리로 돌아오는 데 걸리는 시간이 주기이다.
[4] 면적속도일정의 법칙
- 선분 PR: 점 P에서 타원에 접한 직선(접선)
- 선분 PN: 점 P에서 원에 접한 직선(접선)
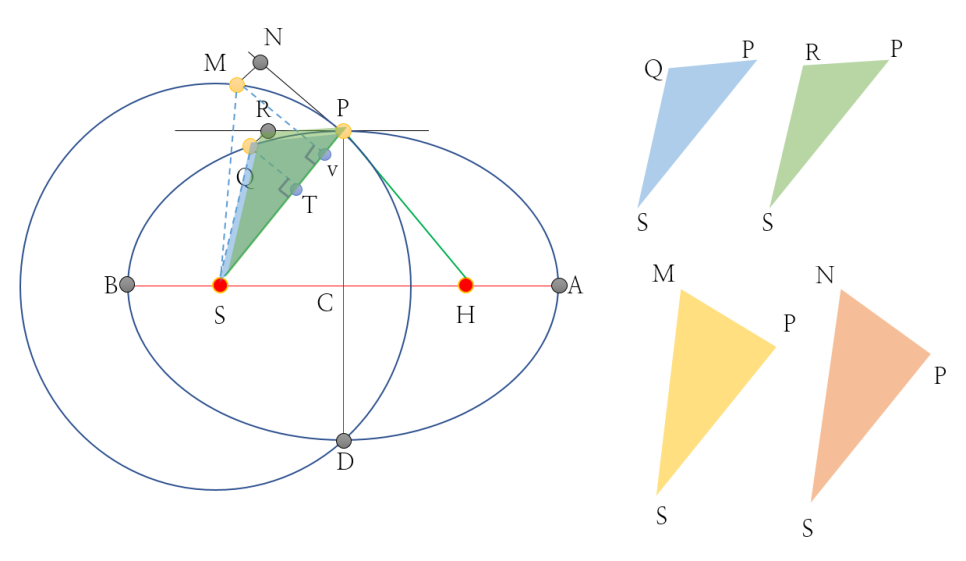
- [그림 2]와 같이, 선분 QR과 선분 MN을 선분 SP와 평행하게 그으면, 삼각형 SQP와 삼각형 SRP를 그릴 수 있다. 행성이 미소 시간 dt에 이동했다 가정했을 때, 둘의 면적은 서로 같고 따라서 Kepler의 면적속도일정의 법칙을 확인할 수 있다.
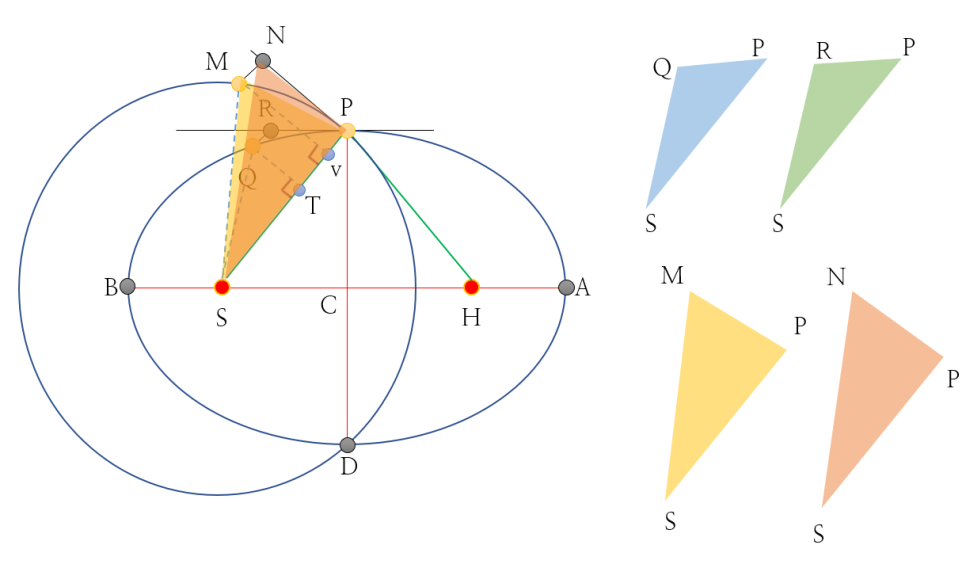
- 마찬가지로 [그림 3]처럼 삼각형 SMP와 삼각형 SNP을 그릴 수도 있는데, 같은 미소 시간 dt을 가정했을 때, 둘의 면적은 서로 같고 Kepler의 면적속도일정의 법칙을 확인할 수 있다.
[5] 「타원궤도를 도는 물체의 만유인력법칙의 기하학적 유도 <Part 2>」에서 우리는 다음 식을 증명하였다.
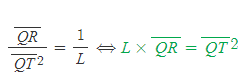
위 식을 유도한 그림의 요소들로 다시 식을 세우면,
로 쓸 수 있다.
- 원 또한 타원의 특수한 경우로 식이 사용될 수 있다.
- L_C는 원의 수직지름을 뜻하는데, 이때 원의 수직지름은 항상 일정하다. ⇒ 원의 지름(2×반지름)
[6] 점 S에 위치한 태양이 작용한 중력은 행성의 궤도와 상관없이 점 P에서는 (1)행성과 떨어진 거리(선분 SP)의 제곱에 반비례하고 (2)그 힘의 방향 또한 선분 SP와 나란하게 S를 향하기 때문에, 행성은 같은 시간 동안 태양으로 떨어진 거리가 모두 같아야 한다.
[7] [과정 5]의 식들을 정리하면,
[8] 도입부에 L을 (선분 PD)^2/2(선분 SP)로 정의했었는데, 이를 [과정 7]의 결과에 대입하면,
이다.
[9] [과정 4]의 삼각형은 행성 P가 원 궤도와 타원 궤도를 돌았다고 각각 가정했을 때, 미소 시간 dt 동안 이동한 면적으로,
로 정리된다.
- 삼각형 SPQ: 행성이 미소시간 동안 타원을 돌 때 훑고 지나간 면적속도
- 삼각형 SPM: 행성이 미소시간 동안 원을 돌 때 훑고 지나간 면적속도
[10] 원의 넓이와 타원의 넓이도 [과정 9]처럼 ratio의 형태로 만들 수 있다.
[11] [과정 9]의 두 행성 움직임의 면적속도 비와 [과정 10]의 한 주기 동안 두 행성이 움직인 면적의 비는 서로 같다. 이를 주기(period) 식에 대입하여 확인하면,
타원의 주기와 원의 주기가 서로 같다는 내용이 증명되고, 앞서 원의 궤도를 도는 행성의 조화의 법칙을 증명하였으므로 타원의 궤도 또한 자연스럽게 궤도의 주기 제곱이 타원궤도의 장반경(선분 SP)의 세제곱에 비례함을 알 수 있다.
'고급물리학' 카테고리의 다른 글
| 【자연철학의 수학적 원리】 제3장. 케플러의 제3법칙 증명 - 원으로 도는 행성 (0) | 2022.02.01 |
|---|---|
| 【자연철학의 수학적 원리】 제2장. 타원궤도를 도는 물체의 만유인력 법칙의 기하학적 유도 <Part 2> (0) | 2022.01.30 |
| 【자연철학의 수학적 원리】 제2장. 타원궤도를 도는 물체의 만유인력 법칙의 기하학적 유도 <Part 1> (0) | 2022.01.30 |
| 【자연철학의 수학적 원리】 제1장. 뉴턴이 정리한 운동법칙 <Part 2> (0) | 2022.01.29 |
| 【자연철학의 수학적 원리】 제1장. 뉴턴이 정리한 운동법칙 <Part 1> (0) | 2022.01.29 |