728x90
반응형


이탈리아의 수학자 토리첼리(Evangelista Torricelli, 1608~1647)는 진공의 존재를 증명하기 위해 1643년 피사에서 아래와 같은 실험을 수행하였다.
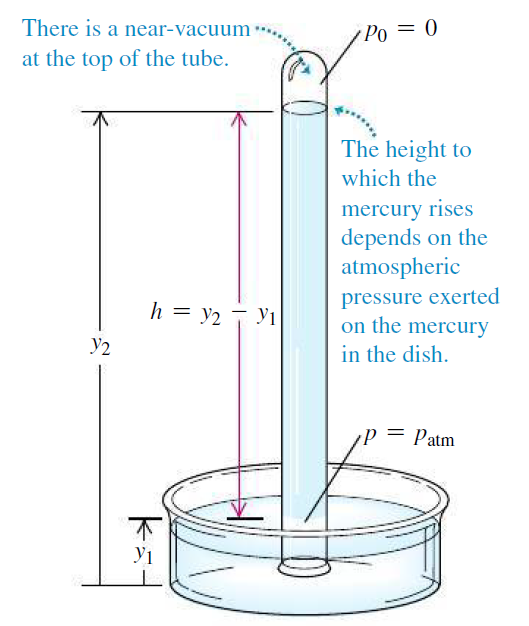
- 토리첼리의 수은 기압계(mercury barometer)[그림 1]: 수은(Hg)으로 채운 긴 관을 뒤집어 수은이 채워진 용기에 수직으로 세운다. 관의 상부는 완전히 막혀있어 위쪽에 생긴 빈 공간은 진공에 가깝고(near-vacuum) 따라서 압력은 0으로 근사할 수 있다.
- 수은 기둥의 시작점과 일치한 지점(A, B)의 압력 p_0는 대기압에 의한 압력과 동일하다.
- [그림 2]의 조건에서 수은 기둥을 생성하는 대기압(B)과 수은 기둥에 의한 압력(A)은 서로 동일하다.
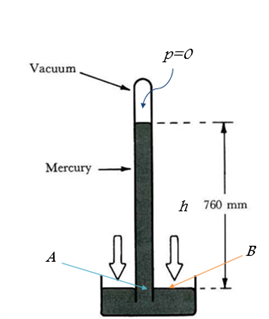
그림 2
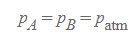
수은 기둥에 의한 압력은 p_A이며, 이는 다음과 같이 계산할 수 있다.
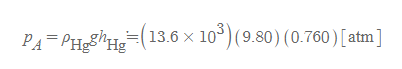
- 1기압이란, 0도씨에서 수은 기둥이 약 0.7600[m]의 높이를 갖는 순간의 압력의 크기와 같다.
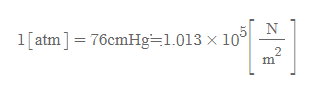
열린 관 수은압력계
Open-tube Manometer
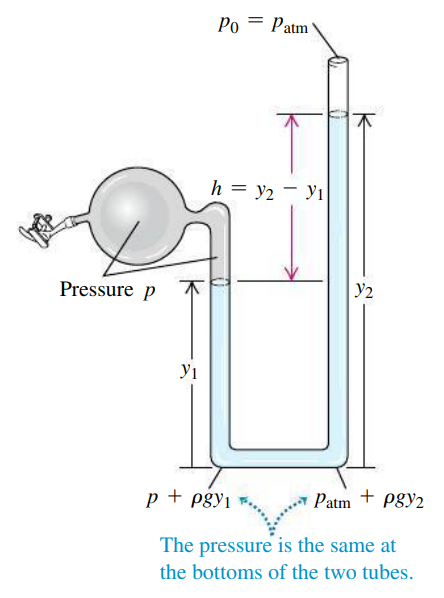
[그림 3]와 같이 생긴 압력계를 '열린 관 수은압력계'라고 한다.
- 오른쪽의 관은 대기압이 들어오는 열려있다.
- 왼쪽의 구 안에는 어떤 기체가 만드는 압력이 존재한다. ⇒ 그 압력은 U자형 관의 왼쪽에 있는 유체에 수직하여 힘을 작용한 결과이다.
- 관의 가장 하단부를 기준으로 압력은 다음과 같이 동등한 값을 갖는다.
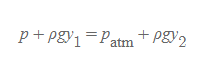
위의 식에 따라, 열린 관 수은압력계에서의 특정한 기체 압력은 아래와 같은 식으로 구할 수 있다.

위의 압력을 계기 압력(gauge pressure)이라 한다.
수은주 밀리미터
mmHg
수은주 밀리리터는 압력의 단위로 기호는 mmHg이다.
- 토리첼리의 실험을 통해 약 1m정도의 긴 시험관에 수은을 채운 것이 시초
- 수은주의 높이에 영향을 줄 수 있는 사항은 두 가지로 (1)해발 고도와 (2)온도를 들 수 있다. ⇒ 온도에 의한 액체의 부피변화가 발생함으로써 전체 높이의 변화를 야기한다.
- 1mmHg는 정확하게 133.322 387 415[Pa]로 정의
728x90
반응형
'고급물리학 > 고전역학 2' 카테고리의 다른 글
| [물리학-고전역학 2] 05. 혈류역학 1 | Hemodynamics (1) (1) | 2023.12.17 |
|---|---|
| [물리학-고전역학 2] 파스칼 법칙 | Pascal's Law (0) | 2023.10.27 |
| [물리학-고전역학 2] 압력 | Pressure (1) | 2023.09.27 |
| [물리학-고전역학 2] 점성 | Viscosity (0) | 2022.01.22 |
| 열에 의한 물질의 팽창 (0) | 2021.11.06 |