
파스칼 법칙
Pascal's Law

프랑스의 수학자 파스칼(Blaise Pascal, 1623~1662)이 발견한 유체정역학의 한 가지 법칙이다.
- 파스칼 법칙: 유체에 의한 압력은 깊이와 유체 표면 압력 p_0의 값에 비례하므로, 유체 표면에 압력을 증가시키면, 압력은 유체 내부의 각 점에 똑같이 전달된다. ⇒ 유체에 작용하는 압력의 변화는 유체 내의 각 점과 용기의 벽에 동등하게 전달된다.
밀폐된 유체에 작용하는 압력은 용기의 벽과 유체의 모든 부분에 같게 전달된다.

파스칼의 법칙[그림 1]

■
유압 프레스(hydraulic press)[그림 2]는 파스칼의 법칙을 활용한 기계이다. e.g. 유압브레이크, 자동차 리프트, 지게차 등에도 응용

유압기의 원리[그림 3]
유압기의 구조에서 단면적의 대소 관계가 A_out<A_in라고 하자. F_in은 단면적 A_in에 가한 힘이고 F_out는 단면적 A_out에 가한 힘을 의미한다. ⇒ F_in은 유압기의 구조 중 압축지점에 가한 힘이다. 그러므로 F_in의 힘에 의해 ‘하강’한 높이를 h_in, F_out의 힘에 의해 ‘상승’한 높이를 h_out이라고 할 수 있다.

일정한 힘을 가하기 때문에 일 W=Fy=Fh식을 따르고, 유체의 마찰이 없는 한, 일은 손실 없이 전달되므로 (Fh)_in와 (Fh)_out의 크기는 서로 같아야 한다.

파스칼의 법칙을 이용하면, F_in, F_out 식을 다음과 같이 유도할 수 있다.

- h_out은 유압기 시스템에서의 실제 물체 이동량으로 물체를 놓은 면적(A_out)이 작을수록 더 많이 이동한다. 즉, 유압기의 상승 및 하강 정도는 유압기의 프레스 단면적의 비를 조정함으로써 구현할 수 있다.
- 유압기의 특성: 사용자가 프레스에 (작은 힘)×(큰 길이)의 일을 수행하면 하면, 프레스는 사용자가 움직이고자 한 물체에 (큰 힘)×(작은 길이)만큼의 일을 수행한다. ⇒ 유압기에서 물체가 놓인 곳(A_out)에 큰 힘(F_out)을 주려면, 유압기의 입력값(h_in)을 크게 해야한다. 유압기에 들어간 input 값에 대해 output은 (1)힘의 이득과 (2)이동거리의 손해로 정리[그림 4]할 수 있다.
- 유압기 내부의 유체 질량은 변하지 않는다.

압력 식을 힘 F(F=pA)에 대해 고쳐쓰고, 이 힘들에 input, output의 개념을 적용하여 일 W=Fh식을 풀어쓰면 아래와 같다.
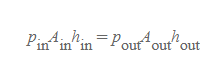
그리고 밀폐된 유체에 작용하는 압력(p)은 용기의 벽과 유체의 모든 부분에 같게 전달되기 때문에, p_in=p_out으로 간주하여 위의 식에서 소거하면,
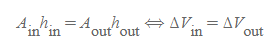
일 식은 결국 유압기의 input 부분과 output 부분의 부피변화율(ΔV)이 일정해야 함을 보여준다.
- 파스칼 법칙의 유압기 input, output 부분의 부피변화율은 항상 일정해야 한다. ⇒ 일반적인 유압기의 A는 고정값이므로, ΔV=(일정)에 기인한 h값의 변동을 예측할 수 있다.
'고급물리학 > 고전역학 2' 카테고리의 다른 글
| [물리학-고전역학 2] 06. 베르누이 방정식(베르누이 법칙) | Bernoulli's Equation (1) | 2023.12.18 |
|---|---|
| [물리학-고전역학 2] 05. 혈류역학 1 | Hemodynamics (1) (1) | 2023.12.17 |
| [물리학-고전역학 2] 토리첼리 실험 | Torricelli's Experiment (0) | 2023.10.27 |
| [물리학-고전역학 2] 압력 | Pressure (1) | 2023.09.27 |
| [물리학-고전역학 2] 점성 | Viscosity (0) | 2022.01.22 |