Herald-Lab
[물리학-고전역학 2] 압력 | Pressure 본문

유체역학
Fluid Mechanics
유체역학(fluid mechanics): 액체, 기체, 플라즈마와 같은 유체의 운동 및 힘의 관계를 다루는 역학의 한 분야 cf. 강체역학
물질의 분류
물질의 종류를 구분[그림 1]하는 한 가지 방법으로 물질에 외력(external force)을 작용해 형태를 변화시키는 데 소요되는 시간을 측정하는 것이 있다.
- 강체(rigid body): 외력이 작용해도 부피나 밀도에 거의 변화가 없는 물질 ⇒ 일반적으로 고체(solid)는 강체로 분류된다. cf. 열기에 의해 녹아내리는 아스팔트
- 유체(fluid body): 약한 응집력(cohesiveness)과 용기 벽이 작용하는 힘에 의해 결합된 무질서한 분자들의 집합 ⇒ 일반적으로 액체와 기체가 유체로 분류된다.

유체역학에서는 유체가 가지는 '특별한 질서'를 크게 다음과 같이 분류할 수 있다.
- 유체 정역학(fluid statics): 정지한 유체가 가지는 질서체계
- 유체 동역학(fluid dynamics): 움직이는 유체가 가지는 질서체계
다루는 유체에 따라서는 다음과 같은 하위 응용학문들이 존재한다.
- 자기유체역학(magnetohydrodynamics): 전자기성을 가진 유체 입자의 거동을 연구하는 학문 e.g. 철강 생산 초기에 불순물을 가진 선철(pig iron) [그림 2] 에 강한 자기장을 걸어 대류를 촉진시킨다.
- 공기역학(aerodynamics): 유체 흐름 중 특히 양력에 대해 집중적으로 다루는 학문, 양력 생성 시 발생할 수 있는 소용돌이, 와류 등에 대해서도 함께 배운다.
- 음향학(acoustics): 음파가 전달되는 매질의 '유동적 특성'을 연구하는 학문, 매질의 유체적 특성을 유체역학을 내용을 적용하여 배운다.
- 양자유체역학(quantum hydrodynamics): 유체역학의 미시적 내용 중 양자역학과 접목이 가능한 내용을 배우는 하위 응용학문, 액체 헬륨의 거동 등을 배운다.

- 혈류역학(hemodynamics): 인간 체내의 혈류의 물리적 특성을 유체역학을 적용하여 배우는 하위 응용학문, 혈관 벽의 동적 특성을 함께 고려하는 데 이는 혈관 벽을 '탄성력을 가진 고체'로 간주하기 때문이다.
압력
Pressure
압력(pressure): 단위 면적 당 '수직으로' 미치는 힘, 스칼라량, 유체 속에 잠긴 물체에 유체가 작용하는 힘의 물리적 특성으로, 물체의 표면 어느 곳에서도 유체가 작용하는 힘은 물체의 표면에 수직한다.

압력
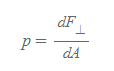
■
- 물리량
- dF_⊥: 물체에 작용하는 유체의 힘으로 물체와 반드시 수직(⊥)하는 요소만을 고려한다.
- dA: 유체의 힘이 작용하는 물체의 표면적(area)
압력은 스칼라량이다. ⇒ 압력을 계산하기 위한 힘의 방향은 면에 수직한 것만 고려하면 된다.
- 단위: [Pa], 파스칼(Pascal)

깊이에 따른 압력
Pressure, and Depth

[그림 4]와 같이 실린더 형 비커에 ρ의 밀도를 가진 정지한 액체가 있고, 수직으로는 깊이가 y인 곳에서부터 y+dy인 곳까지 임의의 유체 요소(element of a fluid) 잠겨있다고 하자. 이때 액체는 유체 요소의 모든 지점에 수직방향으로 힘을 가한다.

유체에 작용하는 힘은 먼저 아래와 같이 구한다.
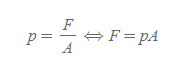
[그림 5]에 따르면 유체 요소의 y축에 작용한 수직한 힘과 일반적 사실은 다음과 같다.
- 유체 요소는 움직이지 않으므로 y축에 작용한 모든 힘의 합은 0이다.
- 유체 요소의 y축에 작용한 힘은 총 세 가지이다. (1)유체요소의 무게(-), (2)유체요소 위쪽에서 누르는(-) 힘, (3)유체요소 아래쪽에서 들어올리는(+) 힘
- 어떤 물체의 무게는 mg이나, 유체의 밀도를 ρ라고 설정하였기 때문에, (밀도)×(부피)=(질량) 식을 응용하여, ρVg라 세울 수 있다.
- y축에 작용한 모든 힘의 합이 0이므로, 결과적으로 아래와 같이 식을 세울 수 있다.


[그림 6]과 같이 유체 요소의 윗면을 2, 유체 요소의 아랫면을 1이라 할 때, (1)윗면의 압력을 p_2, (2)아랫면의 압력을 p_1, (3)유체 요소의 높이를 h=y_2-y_1로 구할 수 있다.

즉, 어떤 유체 요소에 작용한 가장 큰 값의 압력은 물체의 '아랫면'에 작용한 것이고, 값 p_1을 중심으로 깊에 따른 압력 변화량을 아래 식과 같이 쓴다.
깊이에 따른 압력 변화량

■
- 물리량
- p_0: 유체 속 물체의 표면에 작용한 압력
- ρ: 유체 속 '물체'의 밀도
- h: 유체 속 '물체'가 차지한 y축 높이
만약 액체가 대기 중에 노출되어 있다며 대기압(atmospheric pressure)도 고려해야 한다.

'고급물리학 > 고전역학 2' 카테고리의 다른 글
| [물리학-고전역학 2] 파스칼 법칙 | Pascal's Law (0) | 2023.10.27 |
|---|---|
| [물리학-고전역학 2] 토리첼리 실험 | Torricelli's Experiment (0) | 2023.10.27 |
| [물리학-고전역학 2] 점성 | Viscosity (0) | 2022.01.22 |
| 열에 의한 물질의 팽창 (0) | 2021.11.06 |
| 열과 온도 (0) | 2021.11.06 |





