
유체연속방정식
Equation of Continuity for Fluids
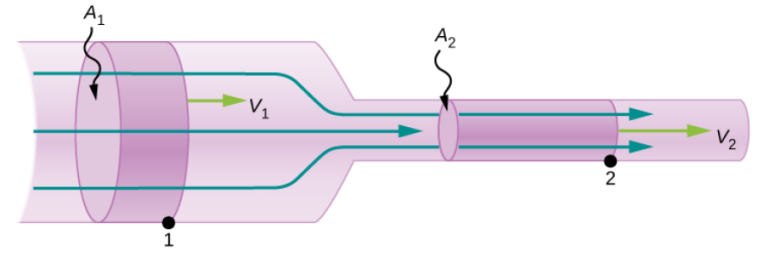
단면적이 서로 다른 관에서 유체 흐름이 갖는 중요한 특징 중 하나는 유체연속방정식(equation of continuity for fluids)을 만족한다는 점이다. 유체연속방정식이란, 유체가 흐르는 관을 따라 흐른 유체의 질량은 [그림 1]의 지점 1과 지점 2에서 모두 동일함을 의미하는 식이다.
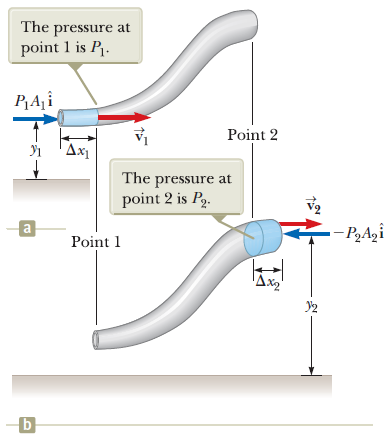
- 지점 1에서 존재하는 유체의 양에 따른 질량 구간은 [그림 2]의 x_1으로 나타난다. 마찬가지로 지점 2에서 존재하는 유체의 질량 구간은 x_2로 나타난다.
- 유체의 질량은 m = ρV인데, 이때 부피는 (단면적)×(높이)이므로, A(단면적) × x(질량 구간)와 같다. 유체의 질량은 원통 실린더 모양을 하고 있다.
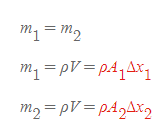
또한 유체의 질량구간인 Δx는 유체가 실제로 관 내부에서 이동하기 때문에, 역학에서의 이동거리 x로 간주하여, (속력) × (시간)의 값으로 바꾸어 표현할 수 있다.
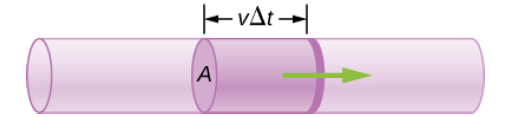
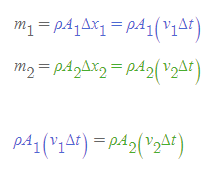
두 질량 m_1과 m_2는 누수가 없으므로 반드시 관에서의 흐른 질량은 서로 같다. 따라서 위의 식을 만족하고 여기서 공통사항인 유체의 밀도 ρ와 유체가 흐른 시간 Δt를 소거하면 유체연속방정식을 최종적으로 유도할 수 있다.
유체연속방정식 | Equation of Continuity for Fluids
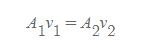
■
유체의 연속방정식에서 유도된 (부피/시간 차원)를 부피선속(volume flux) 혹은 흐름률(flow rate)이라 한다.
- 부피선속 값이 일정하게 측정되었다면, 이 유체는 이상유체에 속하고 또한 중간에 새어나간 유체가 없었음을 의미한다.
베르누이 방정식
Bernoulli's Equation
유체의 경우 어떤 영역을 통과하는 동안 속력이 변하거나 지표로부터 고도가 변하게 되면, 유체의 압력 또한 이러한 변화에 맞추어 같이 변하게 된다. 베르누이 방정식(Bernoulli's equation)은 스위스의 물리학자 다니엘 베르누이(Daniel Bernoulli, 1700-1782)가 1738년에 발표한 내용으로, 유체의 속력과 압력, 그리고 고도 사이의 관계식이다.

베르누이 방정식의 유도 | Derivation of Bernoulli's Equation
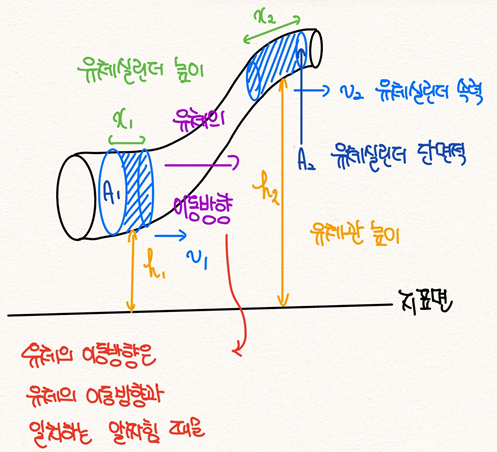
[1] [그림 4]와 같이, 관 안에서 유체가 힘에 의해 지점 1에서 지점 2로 흐를 때, 마찰에 의한 내부에너지의 변화가 없다고 하면 유체 요소는 일-운동에너지 정리를 만족할 것이다.
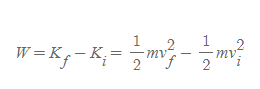
- 특히 관의 단면적이 서로 다를 때는 앞서 배운 유체연속방정식에 따라 관속에서의 유체의 속력이 변한다.
[2] 일의 기본 공식 W=Fs에서 F는 알짜힘을 의미하는데, 유체에 작용한 알짜힘의 경우, 유체의 이동방향과 그 방향이 같은 힘이다. s는 유체 (요소의) 이동거리이다.
[3] 일의 기본 공식에 관의 일반적인 단면적 A/A 항을 대입하여, 식을 아래와 같이 변형한다.
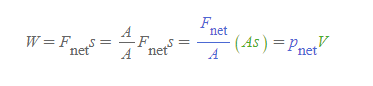
- A/A의 1/A를 F와 곱하면 압력 p가 유도된다.
- A/A의 A를 유체의 이동거리 s에 곱하면, 원통 실린더의 부피 V가 유도된다.
- F가 알짜힘이므로, p또한 유체에 작용한 알짜 압력이 된다. 그리고 이 압력은 유체의 이동방향에는 평행하고, 유체의 단면적에 대해서는 수직한다.
[4] [과정 2]와 [과정 3]의 내용을 조합하고, 이를 원통 실린더의 일반적인 부피 V로 다시 나눈다.
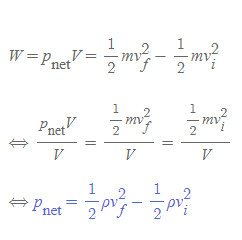
[5] 알짜 압력이란, 유체의 이동방향(오른쪽)에 따라 [그림 4]의 유체 실린더에 대해 A_1번 지점에서 가한 압력이 A_2 지점에서 가한 압력보다 큼을 의미하고, 압력의 정의에 따라 두 힘의 방향은 서로 다름을 유추할 수 있다.
- A_1 지점에 가한 압력의 방향과 A_2 지점에 가한 압력의 방향은 서로 다르다.
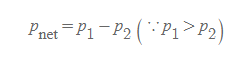
[6] [과정 5]의 내용과 지점 1, 2의 첨자를 반영하여 [과정 4]의 식을 아래와 같이 바꿀 수 있다.
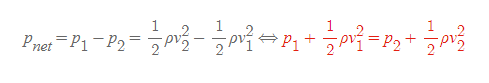
[7] [과정 6]의 식은 유체가 갖는 높이 h에 따른 퍼텐셜에너지를 반영하지 않았다. 그러나 식의 모양에 따라 지점 1과 지점 2의 퍼텐셜에너지는 자연스럽게 아래와 같이 대입될 수 있다.
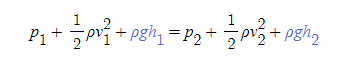
- 중력가속도 g를 포함한 중력퍼텐셜에너지의 질량 m이 밀도 ρ로 바뀌었는데, 이는 [과정 4]에서 모든 항을 일반적인 부피 V로 나누었기 때문이다.
q.e.d.
베르누이의 방정식 | Bernoulli's Equation
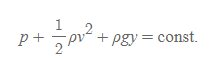
■
- 유체에 가한 일은 (유체의 운동에너지 변화량) + (유체의 퍼텐셜에너지 변화량)의 총합이다.
- 유체의 속력이 증가하면 유체의 압력이 줄어든다.
- 고도가 높아짐에 따라 유체의 압력이 줄어든다. ⇒ 고층 빌딩에서 수도관의 수압이 낮은 이유
'고급물리학 > 고전역학 2' 카테고리의 다른 글
| [물리학-고전역학 2] 08. 혈류역학 2 | Hemodynamics (2) (0) | 2023.12.25 |
|---|---|
| [물리학-고전역학 2] 07. 이상유체와 난류(레이놀즈 수) | Ideal Fluid and Turbulent Flow (0) | 2023.12.24 |
| [물리학-고전역학 2] 05. 혈류역학 1 | Hemodynamics (1) (1) | 2023.12.17 |
| [물리학-고전역학 2] 파스칼 법칙 | Pascal's Law (0) | 2023.10.27 |
| [물리학-고전역학 2] 토리첼리 실험 | Torricelli's Experiment (0) | 2023.10.27 |