
혈류의 층류와 난류
Laminar and Turbulent Flow in a Blood Vessel
혈관에서의 혈액의 흐름은 혈액의 점섬 때문에 [고전역학 2_04. 점성]에서 배운 푸아죄유 법칙을 따른다.
[물리학-고전역학 2] 04. 점성 | Viscosity
유체 내부에서 발생하는 저항력(항력)의 크기는 유체가 가진 점성(viscosity)에 의해 결정된다. 점성: 점도...
blog.naver.com
- 혈액의 점도는 혈구의 비중이 커질 수록 그 수치가 더욱 커지며 이는 비선형적 hematocrit 그래프로 나타난다.
- 혈액의 유량(유량률, 유동률)은 Q로 나타내며 정의는 아래와 같다.

시간간격 Δt동안 관의 단면을 통과한 유체의 전체 부피 V로 dot Q라고 정의한다.

점성을 가진 층류(laminar flow) 혈액의 푸아죄유 법칙[그림 1]은 아래 식을 따른다.
층류 혈액의 푸아죄유 법칙 | Poiseuille's Law of Laminar Blood Flow

■
- 물리량
- Δp: 혈관의 양단에서의 압력 차이
- l: 혈관 길이
- r: 혈관 반지름
- η: 혈액 점성계수
혈류의 유량률 dot Q의 식에서 가장 큰 영향을 미치는 인자는 혈관의 반지름이다. 유량률이 관의 반지름 r에 4배 비례한다는 사실은 동일한 심장 압력 조건에 혈관의 반지름이 1/2이 되면 유량률은 무려 1/16이나 감소하는 것과 같다.
뿐만 아니라 혈액의 η는 혈액 내의 (1)영양소 입자의 농도 및 (2)혈액 속도 v의 증가로 인한 난류 발생 등으로 인해 값이 크게 변할 수 있다. 다만 비압축성 유체의 층류 흐름에서 혈류의 η는 아래 수치 그래프를 비교적 따른다고 알려져 있다.

정상인의 혈액점성은 물의 점성이 1이라 했을 때 약 3(hematocrit=30)[그림 2] 정도의 점성을 가지고 있다고 본다.
혈액의 난류
심장판막이 있는 심혈관의 일부 부위에서는 turbulent flow[그림 3]가 나타나며, 그 결과 유체 내에 작은 소용돌이가 발생한다.
- 관의 반지름이 작아지는 곳에서는 유체의 속도가 점차 증가한다. 이때 증가된 유체의 속도에 의해 혈액의 정상류 특성이 깨지는데, 그 결과 유량률이 줄어드는 turbulent flow가 발생한다.

- 혈류의 속도는 대동맥에서는 약 0.3m/s인 반면, 모세혈관에서는 0.33mm/s에 불과하다. ⇒ 단, 모세혈관은 그 직경이 적혈구 한 개가 겨우 통과할 정도로 매우 작기 때문에 난류에 의한 소용돌이 등은 거의 발생하지 않는다. 또한 느린 속도로 인해 산소와 이산화탄소의 교환이 가능하다.

혈액의 난류는 [고전역학 2_07. 이상유체와 난류]에서 배운 레이놀즈 수에 의해 판단된다.
[물리학-고전역학 2] 07. 이상유체와 난류(레이놀즈 수) | Ideal Fluid and Turbulent Flow
유체 흐름(fluid flow): 유체 유동, 운동 중인 유체의 거동 양상을 뜻하며, 유체의 흐름 성질을 나타내는 ...
blog.naver.com
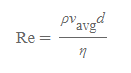
위 식을 속도 v에 대해 풀면, 층류가 난류로 바뀌는 속도(임계속도) 식을 구할 수 있다.
임계속도
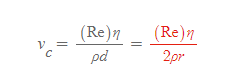
■
- 물리량
- Re: 레이놀즈 수
- η: 유체의 점성계수
- ρ: 유체의 밀도
- v_avg: 유체의 평균 유속
- d: 관의 지름
- r: 관의 반지름
혈액에서 난류는 대개 Re가 2000이 넘어갈 때 발생하는 것으로 계산하므로, 임계속도 식을 다음과 같이 정리할 수도 있다.
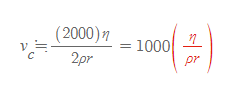
- 위의 임계속도 식은 어떠한 혈관에서 혈액이 흐를 때, 난류가 발생할 때 혈류의 속도를 의미한다.
- 운동 시 심장 박출 혈액량은 약 4-5배 정도 증가하여 혈류의 속도가 급증하는데, 이때는 오랜 시간 임계속도를 초과할 것이다. → 급격한 유속으로 인한 혈류 내 소용돌이 발생확률이 증가하고, 이로 인해 전체 유량률은 오히려 감소할 수 있다.
'고급물리학 > 고전역학 2' 카테고리의 다른 글
| [물리학-고전역학 2] 09. 부력: 아르키메데스 원리 | Archimedes's Principle (0) | 2023.12.27 |
|---|---|
| [물리학-고전역학 2] 07. 이상유체와 난류(레이놀즈 수) | Ideal Fluid and Turbulent Flow (0) | 2023.12.24 |
| [물리학-고전역학 2] 06. 베르누이 방정식(베르누이 법칙) | Bernoulli's Equation (1) | 2023.12.18 |
| [물리학-고전역학 2] 05. 혈류역학 1 | Hemodynamics (1) (1) | 2023.12.17 |
| [물리학-고전역학 2] 파스칼 법칙 | Pascal's Law (0) | 2023.10.27 |

