Herald-Lab
[적분] 20장. 적분표 본문
지금까지 우리는 다양한 피적분함수에 대한 기본적분표 및 적분법(적분전략)을 살펴보았다.
기본적분표
피적분함수의 가장 간단한 형태에 대한 적분 중 특히 부정적분표는 매우 중요하며, 복잡한 형태의 적분의 원활한 풀이를 위해 암기를 요구하기도 한다.
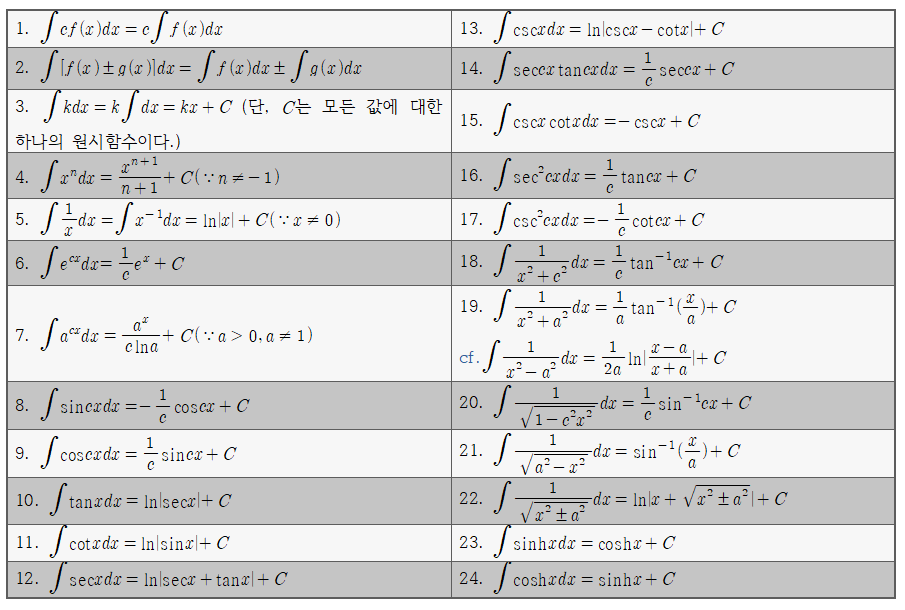
부정적분표를 기본으로 적분의 일반성질 중 아래의 5가지 성질을 특히 주목하도록 한다.

적분의 풀이
부정적분표와 적분의 5가지 일반성질을 기초로 적분은 다음과 같은 풀이과정을 갖는다.
[1] 간단한 피적분함수의 유도한다.

[2] 치환대상을 찾는다.
피적분함수 내에서 u=g(x)로 치환했을 때, 그것의 미분 du=g'(x)dx가 피적분함수의 인수로 곱해진 함수 g(x)를 찾는 것이 좋다.
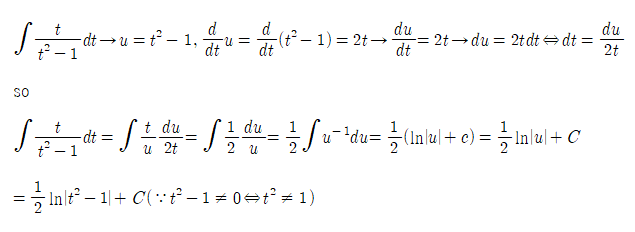
- 적분전략 중 치환적분법을 사용할 수 있다.
[3] 피적분함수의 치환에 실패할 경우, 피적분함수를 형태에 따라 다음과 같이 분류한다.
1. 삼각함수형: 피적분함수 f(x)가 1) sinx, cosx, 또는 2) tanx, secx, 또는 3) cotx, cscx의 거듭제곱이 곱해진 형태라면, 삼각함수적분법을 사용한다.
2. 유리함수형: 피적분함수 f(x)가 유리함수라면, 부분분수적분법을 사용한다.
3. 부분적분형: 피적분함수 f(x)가 x의 거듭제곱 또는 다항식과 삼각함수, 지수함수 또는 로그함수와 같은 초월함수의 곱으로 나타나는 경우, 부분적분법을 사용한다.
4. 무리함수형: 피적분함수 f(x)에 무리함수가 나타나면 다시 두 가지 경우로 나누어 특별한 형태의 치환을 전개한다.
4.1

4.2

적분의 풀이는 [1] → [2] → [3]의 순서로 대부분 해결된다. 특히 치환적분과 부분적분은 가장 기본적인 적분법(적분전략)이므로 반드시 전 과정을 손에 익히도록 한다.
'Calculus > Concepts of Calculus' 카테고리의 다른 글
| [적분] 19장. 적분법: 부분분수적분 - 부분분수분해 (0) | 2019.09.01 |
|---|---|
| [적분] 18장. 적분법: 삼각치환적분 (0) | 2019.08.31 |
| [적분] 17장. 적분법: 삼각함수적분 (0) | 2019.08.30 |
| [적분] 16장. 적분법: 부분적분 (0) | 2019.08.30 |
| [적분] 15장. 적분법: 치환적분 (0) | 2019.08.29 |





