극한의 성질

현대적인 극한의 표기는 영국의 수학자 하디(Godfrey Harold Hardy, 1877~1947, 잉글랜드)의 『A Course of Pure Mathematics』(1908)에서 처음 소개되었다.

 

극한의 성질(properties of limits, limit laws)은 엡실론-델타 논법으로 증명되며, 극한의 사칙연산에 활용된다.

 

극한의 표기

식 1

 

식 1은 x→a(any real number)일 때, 함수 f(x)→L로 향함을 의미한다.

 

극한의 성질

1. 상수함수의 극한(constant function rule): 상수함수의 극한 값은 상수(C) 그 자체이다.

 

 

2. x→a에서 x의 극한(basic limit result)

 

 

3. 샌드위치 정리(squeeze theorem)

 

 

함수의 관계가 다음과 같다고 하자.

 

f(x)≤g(x)≤h(x) for all x close to a

 

x=a인 지점을 제외하고, 조건에서 다음 식을 만족한다.

 

then,

 

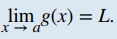
극한의 사칙연산

극한의 사칙연산은 두 개 이상의 극한을 사칙연산할 때 활용된다. 아래 소개할 극한의 사칙연산은 다음과 같다.

 

1. 극한의 합법칙(sum rule)

 

 

두 개 이상의 함수의 극한합(extended sum rule):

 

extended sum rule

 

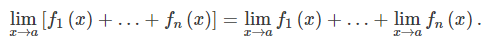
2. 극한의 상수곱법칙(constant multiple): 상수 k가 곱해진 함수의 극한 값은 함수의 극한에 상수를 곱한 값과 같다.

 

 

3. 극한의 곱법칙(product rule)

 

 

두 개 이상의 함수의 극한곱(extended product rule):

 

extended product rule

 

4. 극한의 몫법칙(quotient rule)

 

 

- 극한의 몫법칙은 분모자리의 함수의 극한이 0이되지 않는 조건이 붙는다. (provided that the limit in the denominator function is NOT ZERO)

 

5. 극한의 멱법칙(power rule)

 

 

power rule

 

- where the power p can be any real number.

 

지수함수와 로그함수의 극한

지수함수 극한(limit of an exponential function)

 

 

- 밑(base) b는 0보다 반드시 커야한다.

 

로그함수 극한(limit of a logarithm of a function)

 

 

- 밑 b는 0보다 반드시 커야한다.