[물리학-열역학] 07. 반데르발스(판데르발스) 방정식 (공식 유도 포함) | Van der Waals Equation

 

실제 기체와 반데르발스 방정식

Real Gases and Van der Waals's Equation

 

[열역학_06. 열역학 법칙: 이상기체 상태방정식]에서 배운 내용을 토대로 우리는 이상기체의 특징에 대해서 다음과 같이 정리할 수 있다.

​

https://blog.naver.com/sortie0228/223258881819

 

[물리학-열역학] 06. 열역학 법칙: 이상기체 상태방정식 | Fundamental of Thermodynamics: The Ideal-gas Equation

​

1. 이상기체는 기체 분자 간의 인력이 작용하지 않고, 기체 분자 자체의 부피는 0인 기체이다.
2. 이상기체는 이상기체 상태방정식을 만족하게 거동한다.
3. 이상기체는 모든 압력에 걸쳐 보일의 법칙을 잘 만족한다.[그림 1]

​

3번의 내용은 pV=nRT의 식으로 부터 pV/nRT=Z라고 간주했을 때, 어떠한 압력에서도 값(상수) Z를 만족함을 의미한다.

 

 

 

그림 1. 이상기체는 모든 압력에 걸쳐 보일의 법칙을 잘 만족한다.

 

 

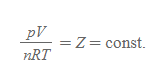
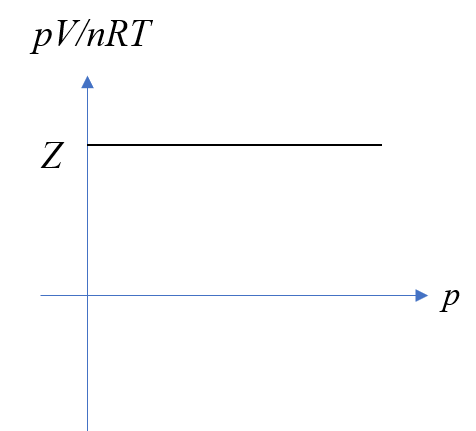
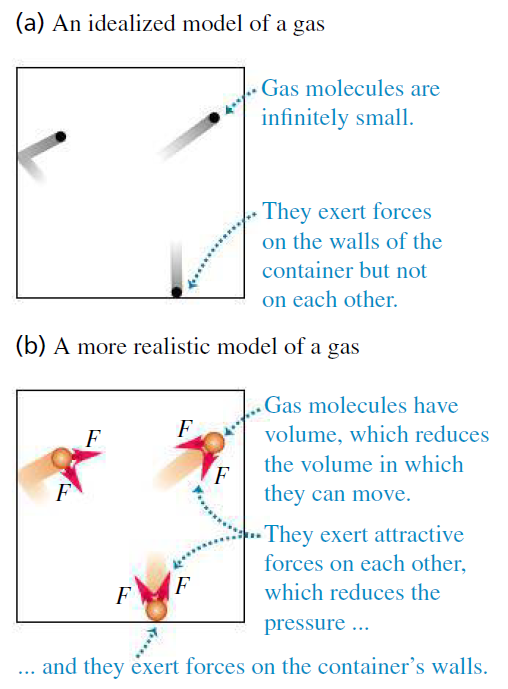
이상의 이상기체의 특징들에 대해 여러가지 반례들을 실제 기체로부터 발견[그림 2]할 수 있다.

1. 실제 기체는 기체 분자 자체의 질량과 부피가 존재하므로, 인력이 작용한다.
2. 실제 기체의 기체분자 자체의 부피 때문에 분자 간의 거리가 매우 가까워지면, 분자 간의 반발력도 급격히 발생한다.
3. 기체 분자 간의 반발력 때문에 더 이상 기체의 부피가 감소하기 어려워지면 이때부터 기체의 부피는 상수가 된다.
4. 기체의 부피가 감소하기 어려워지는 시점에서 압력이 증가하더라도 pV 값은 거의 선형적으로 증가한다.

​

위의 특징은 분자량과 부피가 상대적으로 큰 기체 분자(메테인 등)에 적용된다. 반면 수소 분자와 같이 기체의 분자량이 더 작다면, 기체 분자 자체의 부피로 인한 반발력 요소가 바로 나타난다.

• 기체 분자의 분자량이 클 경우, 어느 정도 인력이 작용한 뒤에 반발력이 급격히 증가한다.
• 반면 기체의 분자량이 작을 경우, 작은 질량으로 인해 인력 인자는 거의 영향력이 없다.

​

그림 2. 이상기체와 실제기체의 거동 차이 [출처: Sears & Zemansky's University Physics with Modern Physics, Young & Freedman, 14th ed., 2016, p.613]

 

 

​

반데르발스 방정식

 

J. D. van der Waals, 1837~1923

 

19세기, 네덜란드의 물리학자 반데르발스(J. D. van der Waals, 1837~1923)가 고안한 실제기체에 대한 근사상태방정식으로 방정식의 형태는 아래와 같다.

​

반데르발스 방정식 | Van der Waals Equation

■

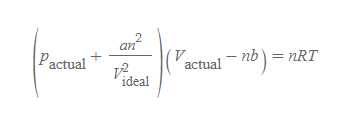
• 정의: 실제기체의 거동에 근사한 값을 유도하는 이상기체 상태방정식의 보정(식)
• 물리량

1. p_actual: 기체 분자에 의한 실제 기체 압력 값
2. V_actual: 기체 분자에 의한 실제 기체 부피 값
3. a: 압력보정상수, 기체에 따라 다른 크기를 갖는 상수로, 분자들 사이의 인력 때문에 발생하는 실제 기체의 낮은 압력을 반영
4. b: 부피보정상수, 기체에 따라 다른 크기를 갖는 상수로, 1몰의 분자들이 차지하는 기체 자체의 부피로

​

​

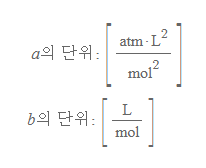
반데르발스 방정식의 유도

[1] n몰의 이상기체의 경우, 기체의 압력은 로 표현할 수 있다.

 

[2] 실제 기체는 (1)분자 자체의 부피와 함께 (2)분자 간의 상호작용이 존재하고, 분자 간의 상호작용은 대부분 분자간의 인력에 의한 것이다. ⇒ 실제 기체의 압력은 분자 간의 인력 요소로 이상기체에서 예상되는 압력보다 작게 측정된다.

• 기체 분자 간의 인력이 서로 작용함으로써 충돌 빈도가 낮아져 '이상기체'에서의 예측 값보다 작게 나온다.

 

[3] 기체의 감소되는 압력 p_d는 (1)이상기체가 차지할 수 있는 부피 V_actual의 제곱에 반비례하고, (2)기체의 몰수에는 제곱비례한다. → 비례상수(압력보정상수) a를 도입해 비례식을 항등식으로 만들 수 있다.

 

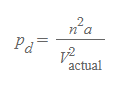
그러므로 p_actual은 다음과 같이 쓸 수 있다.

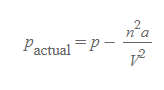
[4] 실제 기체 n몰개의 부피는 분자 자체의 부피요소로 이상 기체에서 예상되는 부피보다 크게 측정된다.

 

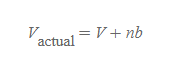
[5] pV=nRT 식은 이상기체가 가지는 p와 V에 대한 내용이었고, 이는 [과정 3]과 [과정 4]의 p_actual, V_actual 식을 변환하여 대입할 수도 있다.

​

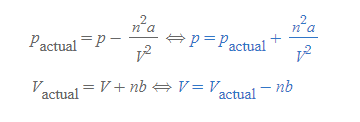
[6] 이상기체 상태방정식에 [과정 5]의 파란색 결과 값을 각각 대입하면 반데르발스 방정식이 최종 유도된다.

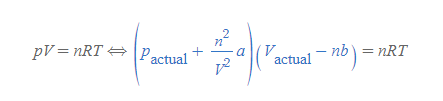
q.e.d.

 

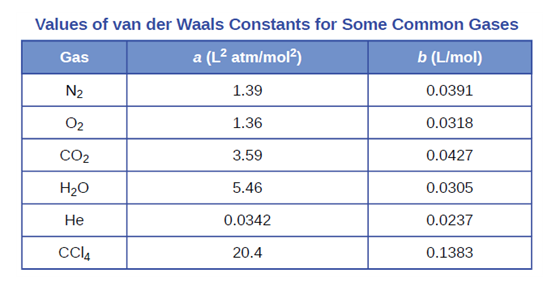
반데르발스 식의 보정상수[표 1]는 실험적으로 측정된다.

 

표 1. 물질에 따른 반데르발스 식 보정상수 표

 

 

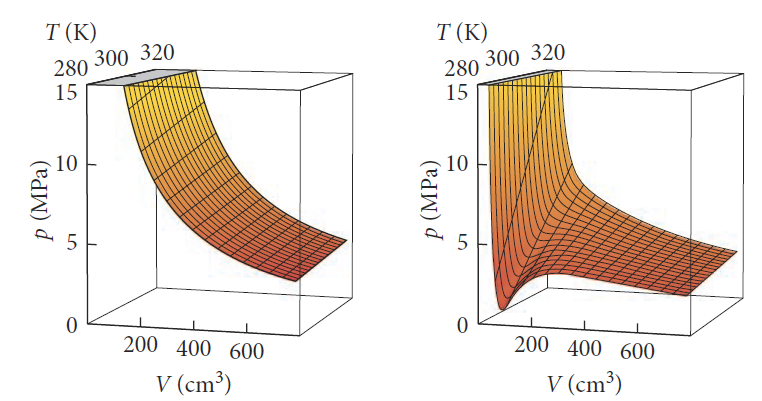
이상기체 상태방정식의 3차원 그래프의 모양 또한 반데르발스 방정식의 내용을 적용하면 [그림 3]과 같이 변한다.

 

그림 3. 이상기체 상태방정식을 만족하는 3차원 그래프와 반데르발스 방정식을 만족하는 기체의 3차원 그래프