고정 헤더 영역
상세 컨텐츠
본문
728x90
반응형
일과 열
Work and Heat
먼저, 열역학적 과정에서 일은 '팽창일'과 '비팽창일'로 크게 분류된다.
- 팽창일: 기체의 부피가 팽창하면서 전하는 일, 기체가 압축될 때는 압축일이라고도 불린다.
- 비팽창일: 전기적인 일 또는 화학적 퍼텐셜에 의한 일
열역학에서의 계의 상태는 압력, 부피, 온도 및 내부에너지와 같은 변수(상태변수)들로 기술된다.
- 에너지가 계의 경계를 통해 전달되는 과정에 있다면 비고립계 조건의 에너지 분석모형 식을 활용하고, 우변에 해당하는 항을 전달변수(transfer variable)로 간주해야 한다.
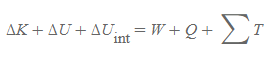
- 경계를 통하는 에너지 전달은 계의 변화를 나타내기 때문에, 계의 주어진 상태가 아닌 계의 상태 변화와 관련된다.
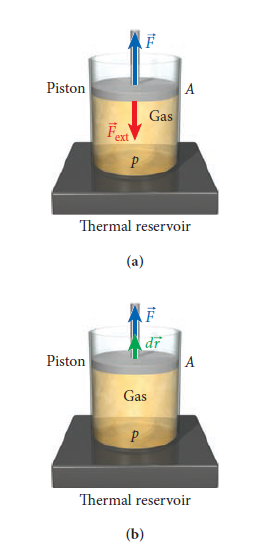
[그림 1]과 같이 피스톤으로 부피를 조절할 수 있는 원통 속에 든 기체를 떠올려 보자. 피스톤은 아랫방향(-)으로 압축 가능하다.
평형상태
평형상태에서 피스톤 내 기체의 부피는 V이고, 원통 벽면과 피스톤에는 같은 크기의 일정한 p가 작용한다.
- 피스톤의 단면을 A라 하면, 기체가 피스톤을 미는 힘은 F=pA로 쓸 수 있다.
준정적 상태
피스톤을 안으로 천천히 밀어 열역학적인 평형상태는 유지하면서 기체를 압축시켜 준정적(quasi-statical) 상태를 만들 수 있다.
- 준정적 과정(quasi-static process)은 계가 매우 천천히 변하여, 각 순간을 평형상태로 간주할 수 있는 이상적인 과정을 의미한다.
- 피스톤을 아래로 미는 경우[그림 2], 일의 정의에 따라 피스톤(외력에 의해 움직이는)이 기체에 한 일은 다음과 같이 계산한다.
피스톤-기체 시스템에서의 일
[1] 외력에 의해 피스톤이 기체에 한 (미소)일은 아래 식과 같다.
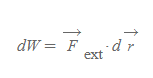
[2] 실린더 내의 기체는 외력에 대해 반대 방향으로 힘을 작용하므로, 기체가 피스톤에 한 일은 다음과 같이 쓸 수 있다.
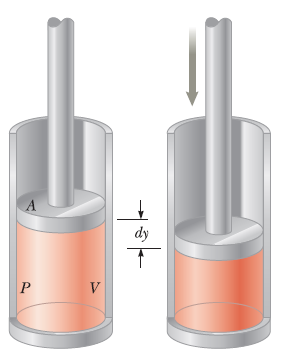
[3] 기체가 피스톤을 미는 힘의 크기는 F=pA이다. 여기서 A는 피스톤의 단면적과 같다.
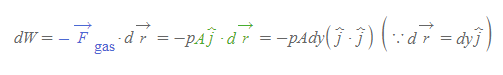
[4] [과정 3]의 Ady는 피스톤의 미소부피 dV과 같다.
[5] 미소 일 식을 기체가 한 전체 일 식으로 바꾸기 위해서 적분을 취해준다. [과정 4]의 오른쪽 항의 미소변화량은 부피로 변하였음에 유의한다.
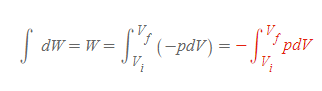
피스톤이 기체에 한 일 | Work done on a Gas
■
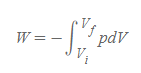
- 피스톤이 기체에 한 일의 부호
- 기체가 압축되면 dV는 (-)이고 (외력이) 기체에 한 일은 결국 (+)가 된다.
- 기체가 팽창하면 dV는 (+)이고 (외력이) 기체에 한 일은 (-)가 된다.
위의 식은 일을 하는 주어를 기체로 바꾸었을 때, 다음 논리구조를 갖는다.
실린더 부피의 팽창은 실린더 내 기체가 일을 하기 때문이고, 이는 (1)W가 양수부호를 가져야 함을 뜻한다. 또한 (2)부피을 반영해 dV 또한 양수부호를 가져야 하는데, 이 때문에 피스톤이 기체에 한 일 식에서 (-)부호만 제거하면 기체가 피스톤에 한 일 식을 유도할 수 있다.
기체가 피스톤에 한 일 | Work done by a Gas
■
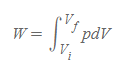
- 의미: 기체가 피스톤에 대해 한 일로 시스템 내부에서 기체는 (1)압축과 (2)팽창을 반복할 수 있다.
- 팽창(expansion) 시 기체가 한 일은 (+)이고, 압축(compression) 시 기체가 한 일은 (-)이다.
특히 두 번째 식은 기체를 주어로 삼았으므로, 이상기체 상태방정식을 적용하여 W 식을 다음과 같이 수정하여 적을 수도 있다.
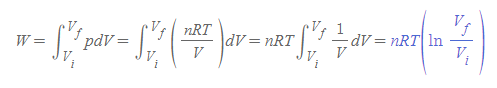
기체가 피스톤에 한 일 | Work done by a Gas
■
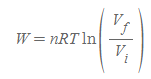
- V_f이 V_i보다 큰 경우(팽창), 마찬가지로 W는 양수 부호를 만족한다.
마지막으로 p와 V는 서로 반비례한다는 관계를 위의 식에 적용하면, 기체가 피스톤에 한 일은 또한 아래와 같이 쓸 수도 있다.
기체가 피스톤에 한 일 | Work done by a Gas
■
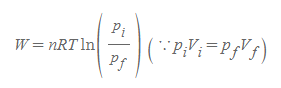
pV 도표
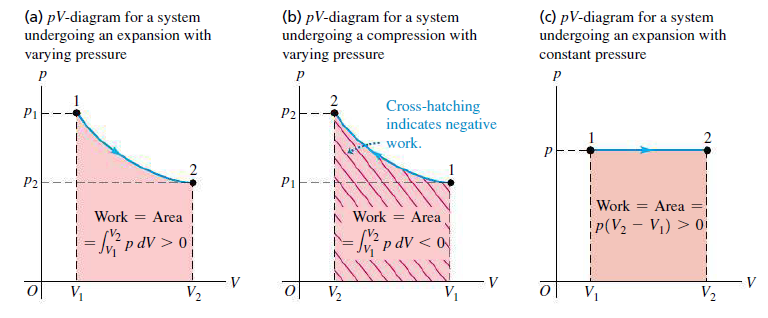
pV 도표(pV diagram): 기체가 지나가는 과정 동안 각 단계에서의 압력과 부피를 알면 기체의 상태를 그래프[그림 3]로 표현할 수 있다.
- x축: 부피
- y축: 압력
기체의 준정적 과정에서, 기체가 한 일은 pV 도표에서 처음 상태와 나중 상태 사이의 곡선 아래의 넓이와 같다.
- 처음상태에서 나중상태로 가는 동안 기체에 한 일은 두 상태 사이의 경로에 따라 달라진다. ⇒ 일의 경로의존성
728x90
반응형
