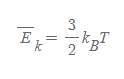몰 수와 아보가드로 수
Avogadro's Number
몰(mole): 순수한 화학원소에서부터 화합물까지 1몰 단위에는 모두 같은 수의 분자가 들어있다.
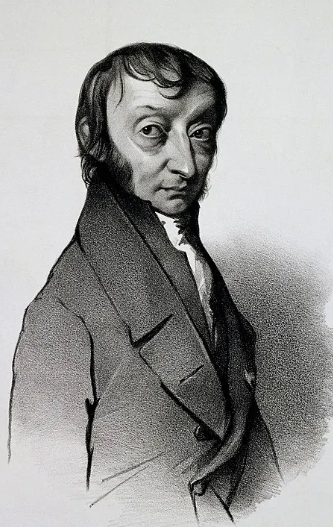
이탈리아 샤르데냐 왕국 출신의 화학자 아보가드로는 자신의 이름을 딴 아보가드로의 법칙 이외에도 (1)몰의 개념과 (2)분자설을 함께 주장하였다.
아보가드로 수(Avogadro's number, constante di Avogadro): 1몰의 정확한 정의로, 1몰이란, 원자량이 12인 탄소 0.012kg에 들어있는 원자수와 같은 수의 물질의 양이다.
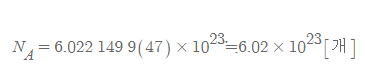
그리고 아보가드로 수를 사용하여 몰 수 n을 표현하면 다음과 같다.
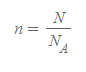
- N은 실제 물질의 주어진 양이다. 이를 아보가드로 수로 나누면 몰 수 n을 계산할 수 있다.
다음 [열역학_06. 열역학 법칙: 이상기체 상태방정식]에서 배운 시료 질량의 공식을 n에 대해 재정리하면 다음과 같다.
[물리학-열역학] 06. 열역학 법칙: 이상기체 상태방정식 | Fundamental of Thermodynamics: The Ideal-gas Equation
이상기체 이상기체(ideal gases): 기체의 상태방정식(equations of state)에 완벽하게 기인하여 거동하는 ...
blog.naver.com
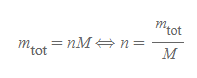
- M은 몰질량으로 어떤 물질이 1몰개 만큼 있을 때 질량(mass of 1 mole of ...)을 의미한다.
두 개의 공식은 공통적으로 몰 수 n을 계산하기 위한 방법으로 둘의 관계는 동시에 등가이다.
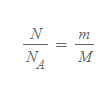
몰 질량으로 표현한 시료 질량
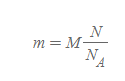
■
- 의미: 시료 질량은 1몰 개가 존재할 때 정확하게 몰 질량과 일치한다.
볼츠만 상수
Boltzmann's Constant

오스트리아의 물리학자 볼츠만(Ludwig E. Boltzmann, 1844-1906)이 기체 분자의 통계역학을 정리하다 유도한 개념으로, 그의 상수는 이상기체 상태방정식의 n을 기체 분자의 전체 개수 N으로 치환함으로써 매우 쉽게 유도된다.
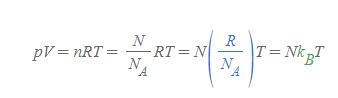
몰수는 전체 분자 수를 아보가드로수로 나눈 값과 같기 때문에 위와 같이 식을 고칠 수 있고, N_A와 R은 모두 크기가 정해진 상수이기 때문에 이들을 따로 묶을 수 있다.
볼츠만 상수 | Boltzmann's constant

■
- 단위가 [J/K]이기 때문에 이후 배우게 될 엔트로피의 정의와도 동일한 차원을 갖는다.
볼츠만 상수의 활용
이상기체 상태방정식
먼저, 볼츠만 상수를 활용하여 이상기체 상태방정식를 다음과 같이 표현할 수 있다.

특정한 에너지를 가진 기체들의 분포 확률
또한, 볼츠만 상수는 온도가 T로 측정된 방안에 있는 기체 분자 시스템의 에너지가 특정한 값인 E일 확률을 구하는 데 매우 중요하게 활용된다.
- 통계역학의 시작은 볼츠만 인자(Boltzmann factor)에서 나왔다고 할 정도로 혁신적인 개념으로 기체 분자의 여러가지 상태를 고전적인 물리 수준에서 매우 성공적으로 해석했다.
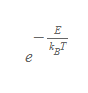
- 볼츠만 인자의 e는 자연로그의 밑(오일러 수, Euler's number)을 의미한다.
정준분포(canonical distribution)란, 입자들이 특정한 에너지를 보유할 확률들의 분포로 P(E)라 쓰고 이 값은 볼츠만 인자와 비례한다.
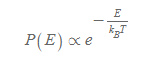
기체분자의 평균 병진운동에너지
기체분자의 고전적 운동 역학에서 추후 배우겠지만, 기체분자들이 지닌 평균 병진운동에너지를 avarage E_k라 했을 때, 그 값은 온도만의 함수이고, 등식으로 풀어쓸 때 k_B가 포함된다.