Herald-Lab
【미분적분학 2】 Chapter 10. 부분분수분해 본문

부분분수 적분은 피적분함수가 유리함수(분자와 분모가 다항식으로 이루어진 함수)꼴인 함수를 쉽게 적분하는 전략이다.
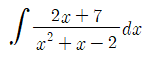
식 19.1
식 19.1의 피적분함수는 유리함수이고, 이 유리함수는 인수분해를 통해 간단한 분수의 합(식 19.2)으로 나타낼 수 있다.
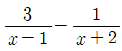
식 19.2
식 19.2를 연산하면 식 19.1의 피적분함수를 다시 구할 수 있고, 이 과정의 역(역과정)이 즉 부분분수분해(Partial Fraction Decomposition)이다.
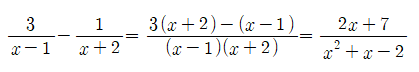
분수의 구분
유리함수는 일반적으로 다음과 같이 표현한다.
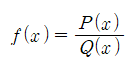
여기서 P와 Q는 다항식으로 P의 차수(degree)가 Q의 차수보다 작을 때, f는 더 간단한 분수의 합으로 표현된다.
- 진유리함수(proper rational fraction): P(x)의 차수가 Q(x)의 차수보다 작은 유리함수
a_n≠0일 때 다항식,
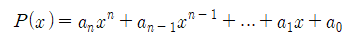
에 대해 P의 차수를 n이라 하고, deg(P)=n으로 나타낸다.
(1) 진(proper)분수: 분모의 차수가 분자의 차수보다 큰 분수, deg(P)<deg(Q)
(2) 가(improper)분수: 분자의 차수가 분모의 차수보다 크거나 같은 분수, deg(P)≥deg(Q)
improper fraction의 경우, deg(R)<deg(Q)인 나머지 R(x)가 얻어질 때까지 P를 Q로 나누는 다항식의 나눗셈을 수행해야 한다. 나눗셈의 몫을 S(x)라 하면 연산의 수행 후 가분수는,
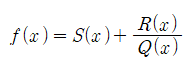
와 같은 형태로 나온다.
- S(x): 몫
- R(x): 나머지
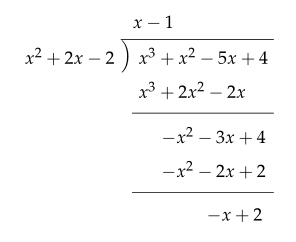
다항식의 나눗셈
|
제시된 다항식의 나눗셈(P÷Q)에서 몫과 나머지는 다음과 같다.
- S(x)=x-1
- R(x)=-x+2
- Q(x)=x^2+2x-2
|
다항식의 나눗셈을 마친 후, 분모인 Q(x)를 가능한 만큼 인수분해 하도록 한다. 임의의 다항식 Q(x)는 일차인자(ax+b)나 기약 이차인자(ax^2+bx+c, b^2-4ac<0)의 곱으로 인수분해된다.
조립제법
다항식을 나눌 경우, 다항식을 직접 나누지 않고 계수(coefficient)만을 이용해 나눗셈을 해 몫과 나머지를 구할 수 있다. 이탈리아의 수학자 루피니가 1809년 처음으로 고안했다.

Paulo Ruffini (1765~1822, 이탈리아)
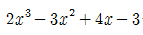
식 19.3
식 19.3을 x-1로 나눈다고 생각해보자.
1. 식 19.3의 각 계수를 차례로 적는다. ⇒ 2, -3, 4, -3
2. x-1=0이 되게 하는 x의 값을 적는다. 조건을 만족하는 x는 1이다.
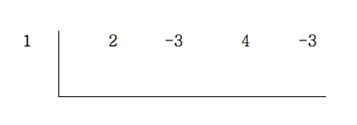
3. 첫 값 2는 그대로 아래로 내려 적는다.
4. 내력 적은 2와 왼쪽의 1을 곱해 계수 -3 아래에 기입한다.
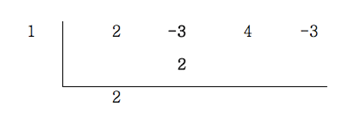
5. -3과 2를 '더한' 값을 아래에 적는다.
6. 내려 적은 더한 값 -1을 다시 왼쪽의 1과 곱해 계수 4 아래에 기입한다.
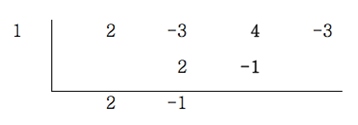
7. 이 순서를 반복하면 조립제법 표가 완성된다.
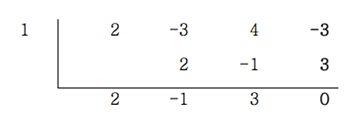
조립제법 표
8. 마지막 행에 쓰인 숫자들은 다항식의 나눗셈 몫 계수와 나머지가 된다.
- 최하단 행의 2, -1, 3은 몫의 계수를 의미한다.
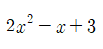
몫
- 최하단 행의 가장 오른쪽 숫자는 나머지를 의미한다. 위의 조립제법 표에서 나머지는 0이다.
부분분수분해
부분분수의 분해는 분모의 형태에 따라 크게 5가지 풀이법을 갖는다.

부분분수분해를 통해 유리함수의 더 쉬운 적분이 가능해진다.
'미분적분학 > 적분' 카테고리의 다른 글
| 【미분적분학 2】 Chapter 9. 삼각치환적분 (0) | 2024.11.23 |
|---|---|
| 【미분적분학 2】 Chapter 8. 삼각함수적분 (0) | 2024.11.22 |
| 【미분적분학 2】 Chapter 7. 부분적분 (0) | 2024.11.21 |
| 【미분적분학 2】 Chapter 6. 치환적분 (0) | 2024.11.20 |
| 【미분적분학 2】 Chapter 5. 부정적분 (0) | 2024.11.18 |





