반응형
250x250
Notice
Recent Posts
Recent Comments
Link
Herald-Lab
【물리학 - 고전역학】 05. 좌표계 본문
728x90
반응형

물리학의 여러 가지 문제 상황은 공간 상에서의 위치 표현으로부터 시작된다.
- 공간 상의 위치표현은 프랑스의 철학자 르네 데카르트(René Descartes, 1596-1650)가 저술한 『기하학(La Geometrie)』(1637)과 프랑스의 법조인 페르마(Pierre de Fermat, 1607-1665)의 3차원에 관한 연구로부터 발전되어 왔다.
- 특히 데카르트의 직각좌표계 발명[그림 1]은 이후 유클리드 기하학과 대수학을 연결하는 데 결정적이었던 것으로 평가된다.


좌표계(coordinate system): 물리량의 값(수치)을 공간 상 좌표로 표현하기 위해 도입한 체계, 물체의 운동을 기술할 때 반드시 필요하다.
- 좌표(coordinate): 좌표계에서의 물체의 운동 및 그 위치에 부여된 수치, 성분
- 해석기하학에서는 특정한 한 점이 좌표(x, y, z)로 표현되면서, 도형의 성질을 방정식으로 풀어낼 수 있게 되었다.
좌표계의 도입
좌표계에서의 점은 실수 순서쌍(ordered pair, ordered set)으로 간주된다.
- 순서쌍이란, 순서가 고려되는 둘 이상의 변수로 일반적으로 (a, b)로 표현된다.
- x축(x-)과 y축(y-)의 두 축 시스템(직각좌표계)에서 좌표 (x, y)는 (a, b)로 표현되며, (a, b) ≠ (b, a)이다.
- 직선, 곡선, 평면은 그 형태에 따라 방정식으로도 표현 가능하다.
- 도형의 성질 또한 방정식의 형태로 설명하고, 방정식의 해(solution)는 기하학적인 대상이 된다.
2차원 좌표계의 종류
고전역학의 많은 문제는 평면 2차원 좌표계로 풀리며, (1)평면직각좌표계(데카르트 좌표계)와 (2)평면극좌표계(극좌표계)가 대표적이다.
<데카르트 좌표계>

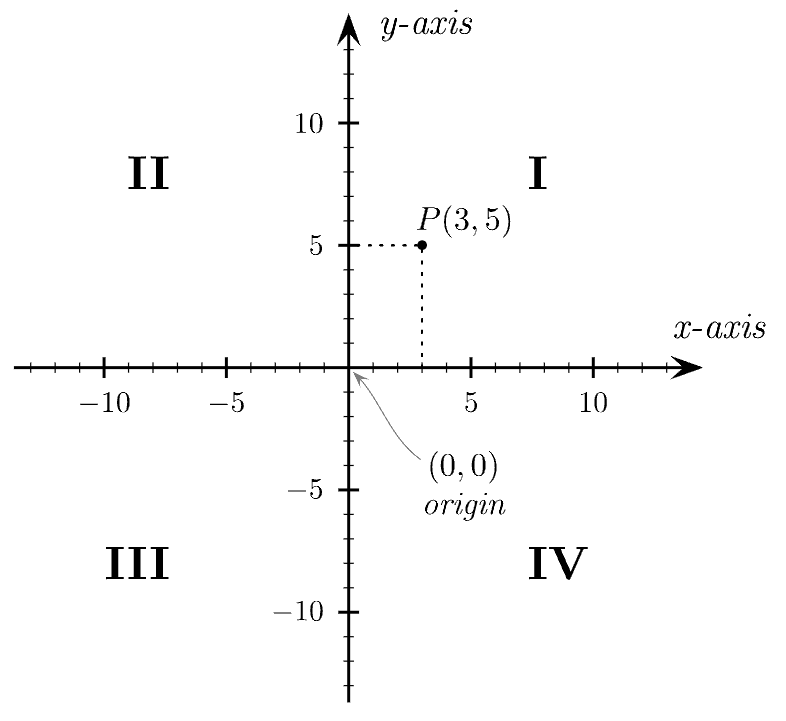
데카르트 좌표계: 평면직각좌표계로 [그림 2]와 같은 형태를 띤다. 이차원 상에서 원점 O(0, 0)을 기준으로 서로 수직한 두 축을 그린 좌표계
- 원점을 기준으로 임의의 한 점 P는 (x 좌표, y 좌표)로 표기한다.
- 데카르트 좌표계의 두 축에 의한 임의의 평면을 좌표평면이라 한다.
- [그림 1]과 같이 좌표평면은 크게 4개의 사분면(일사분면 Ⅰ, 이사분면 Ⅱ, 삼사분면 Ⅲ, 사사분면 Ⅳ)으로 구분된다.
<극좌표계>

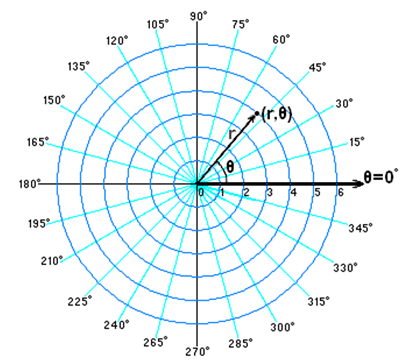
극좌표계: 평면극좌표계라고도 불리며 평면상의 한 점을 표현할 때, (1)직각좌표의 원점으로부터 한 점의 특정 위치인 (x, y)까지의 직선거리 r과 (2)원점에서 주어진 점까지 그은 선분과 고정된 x-사이의 각도 θ를 활용해 점의 위치[그림 4]를 표현할 수 있다.
- 극좌표계에서 원점을 기준으로 임의의 한 점 P는 (r 좌표, θ 좌표)로 표기한다.
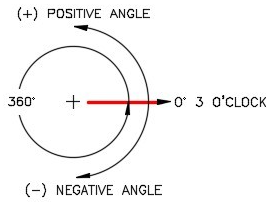
- 고정축은 +x축(+x-)으로 잡고, 각도는 반시계 방향을 (+)부호로 측정한다. [그림 5]
- +θ: 양각(positive angle), 고정축 +x-으로부터 반시계 방향으로 잰 각도
- -θ: 음각(negative angle), 고정축 +x-으로부터 시계 방향으로 잰 각도
2차원 좌표계의 변환
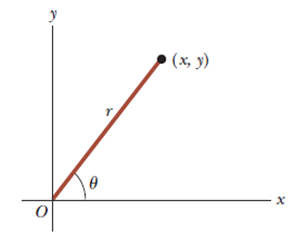
데카르트 좌표계와 극좌표계는 모두 2차원의 평면에서 같은 점[그림 6]을 다른 좌표 요소로 표현하는 것이다. 따라서 이들은 서로의 좌표 값을 통해 유도될 수 있다.
직각좌표를 극좌표로 변환하기
직각좌표 x, y 값을 이용하여 극좌표 r, θ를 유도할 수 있다.
- 좌표 유도를 위해 [그림 7]의 삼각법(trigonometry) 지식과 피타고라스 정리(Pythagorean theorem)를 활용해야 한다.

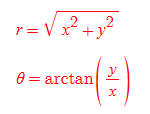
극좌표를 직각좌표로 변환하기
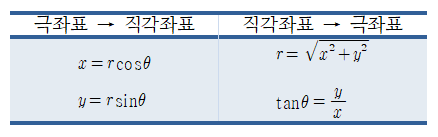
위와는 반대로, 극좌표 r, θ 값을 이용하여 직각좌표 x, y를 또한 유도할 수 있다.
- 좌표 유도를 위해 마찬가지로 삼각법의 지식을 활용한다.

728x90
반응형
'고급물리학 > 고전역학' 카테고리의 다른 글
| 【물리학 - 고전역학】 07. 벡터 <PART 1> (0) | 2025.06.02 |
|---|---|
| 【물리학 - 고전역학】 06. 차원과 스칼라 (0) | 2025.06.01 |
| 【물리학 - 고전역학】 04. 위치, 속력, 속도 (0) | 2025.05.28 |
| 【물리학 - 고전역학】 03. 단위변환과 유효숫자 (0) | 2025.05.27 |
| 【물리학 - 고전역학】 02. 기본물리량 (0) | 2025.05.25 |





