반응형
250x250
Notice
Recent Posts
Recent Comments
Link
Herald-Lab
[물리학-전자기학] 31. 비오-사바르 법칙 | Biot-Savart Law 본문
728x90
반응형

비오-사바르 법칙
Biot-Savart Law
프랑스의 두 물리학자 비오(Jean-Baptiste Biot, 1774~1862)와 사바르(Félix Savart, 1791~1841)가 외르스테드의 발견(1819) 직후, 전류가 근처 자석에 미치는 힘에 관한 실험을 수행했다.


- 발견: 공간의 한 점에 전류에 의해 만들어지는 자기장을 전류의 함수로 표현


- 물리량[그림 1]
- d(벡터 B): 미소 자기장
- I: 정상전류 조건
- d(벡터 s): 도선의 길이 요소
- r: 도선의 한 지점과 측정하고자 하는 자기장이 있는 위치 사이의 거리, [그림 2]에 따라, [그림 1]의 위쪽 P에서는 자기장이 지면을 '나오는 방향'으로 형성되는 반면, 아랫쪽 P는 지면을 뚫고 자기장이 '들어가는 방향'으로 자기장이 형성된다.

비오와 사바트는 비례식을 등식으로 만들어 주기 위해 상수 k를 실험적으로 아래와 같이 특정했다.

- μ_0: 자유공간의 투자율(permeability of free space)
- 투자율이란, 매질에 따른 자성의 특성 차이를 설명하는 비율로 자유공간의 투자율이란, 진공 중에 가한 외부의 자기장에 의해 진공에서 자기 유도가 일어나는 정도를 말한다.
비례식과 k의 값을 합쳐 비오-사바르 법칙을 아래와 같이 정리할 수 있다.
비오-사바르 법칙
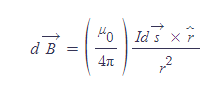
■
- 물리량
- I: 정상 전류 조건
- d(벡터 s): 도선의 길이요소, 전류방향과 일치한다.
- d(벡터 B): d(벡터 s)에서의 전류 I에 의한 점 P에서의 미소 자기장
- r: 미소 도선 요소와 미소 자기장 사이 떨어진 거리
- μ_0: 자유공간의 투자율
비오-사바르 법칙에서 Id(벡터 s)는 합쳐서 전류 요소(current element)라고 하는데, 이 항이 P 지점에 자기장을 형성하는 원인이 된다.

비오-사바르 법칙의 해석
비오-사바르 법칙 공식에서 확인할 수 있는 실험 결과는 다음과 같다.

결국 미소 전류요소에 의해 미소 자기장이 비례한 값으로 형성되는 것이 비오-사바르 법칙의 핵심이다.
비오-사바르 법칙의 크기는 벡터곱을 풀어쓴 것과 같다.

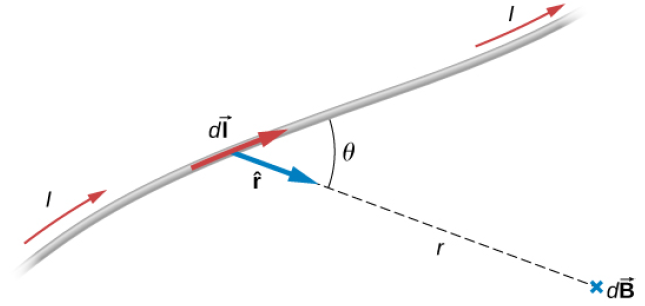
- 단위벡터 r의 크기는 1이기 때문에 크기 식에서 생략되고, θ는 미소 전류요소와 단위벡터 r 사이의 최소각[그림 3]이다.
비오-사바르 법칙은 미소 전류요소에 의한 미소 자기장을 구하는 공식으로, 유한한 크기의 전류에 의한 임의의 점에서의 전체 자기장을 구하기 위해서는 전류를 구성하는 모든 전류요소로부터 만들어지는 미소 자기장들을 모두 합해야 한다.
유한한 크기의 전류에 의한 점 P에서의 전체 자기장
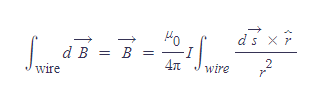
728x90
반응형
'고급물리학 > 전자기학' 카테고리의 다른 글
| [물리학-전자기학] 32. 앙페르의 법칙 | Ampere's Law (0) | 2024.01.20 |
|---|---|
| [물리학-전자기학] 30. 자기력 1 | Magnetic Field Force (1) (1) | 2024.01.07 |
| [물리학-전자기학] 29. 자기력선 | Magnetic Field Lines (0) | 2023.12.01 |
| [물리학-전자기학] 28. 자석과 자성 | Magnets and Magnetism (0) | 2023.11.30 |
| [물리학-전자기학] 27. RC회로의 특징과 시간상수(시상수) | Features of RC Circuits and Time Constant (0) | 2023.11.20 |




