Herald-Lab
[물리학-고전역학] 뉴턴의 발견 - 중력의 법칙 | Law of Gravity 본문

천체역학(celestial mechanics): 고전 역학의 원리를 천문학 분야에 응용하여 천체의 운동을 연구하는 물리학 또는 천문학의 한 분야
「Celestial mechanics is the branch of astronomy that deals with the motion of objects in outer space. Celestial mechanics applies principles of physics to astronomical objects, such as stars and planets, to produce ephemeris data.」

잉글랜드의 위대한 수학자이자 물리학자인 뉴턴 (Sir. Isaac Newton, 1642-1727) 은 달을 지구로 돌게 하는 원인은 힘이며, 이 힘이 물체의 속도를 변화시킨다고 주장했다. 뿐만 아니라, 1687년 그는 지구와 달 사이에 작용하는 힘인 중력의 법칙(law of universal gravity)을 다음과 같이 발표했다.
"우주에 존재하는 물질의 모든 입자는 모든 다른 입자들을 잡아당기는데, 이때 서로 잡아당기는 힘을 인력이라 하며, 그 힘의 크기는 입자들의 질량에 곱에 비례하며, 그들 사이의 거리의 제곱에 반비례한다." (Newton, 1687)
동역학
Dynamics
동역학(dynamics): 물체 운동에 영향을 주는 원인인 힘(force)과 질량(mass)에 대한 역학의 세부분야
- 힘이 항상 운동을 유발시키지는 않는다. 예를 들어, 우리가 의자에 앉아있을 때 우리는 중력과 수직항력을 동시에 받음으로써 정지한 운동상태를 가질 수도 있다.
- 운동학(kinmatics): 운동의 수학적인 표현을 다룬 동역학의 세부분야
- 운동역학(kinetics): 운동을 발생시키는 힘과 관련한 고전역학의 다양한 물리법칙을 다룸, 주요한 해석 방법은 크게 (1)힘-질량-가속도 법, (2)일-에너지 법, (3)충격량-운동량 법으로 나뉜다.
뉴턴은 달이 지구 주위로 돌게 하는 원인으로 '힘'을 꼽았으며, 힘은 궁극적으로 물체의 속도를 변화시킨다고 생각했다.
- 운동학에서 속도의 변화는 속도의 크기인 (1)속력과 (2)방향의 변화로 크게 구분할 수 있다.
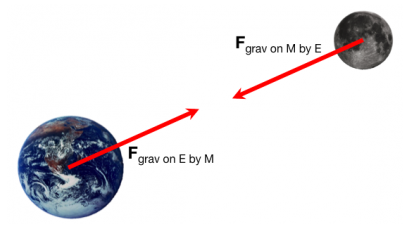
- 지구와 달 사이에는 힘[그림 1]이 작용하는 데 이를 기하학적으로 분석해 중력의 역제곱 법칙을 유도함
힘의 분류
- 접촉력(contact force): 두 물체 사이의 물리적인 접촉을 수반한 힘
- 장력(field force): 비접촉력, 두 물체 사이의 물리적 접촉 없이 작용하는 힘으로 필드(field) 또는 장을 매개로 한다. 전기장, 자기장 등이 대표적이다.
- 물체가 가진 질량과 전하는 고유한 속성으로 물체 주변 공간을 왜곡시키는 장을 만든다. 공간적 왜곡은 마치 일상생활의 경사(slope)와 같이 작용하는데, 경사가 놓인 제3의 물체는 기울기에 따라 (움직임) 속도를 가지며, 이러한 움직임은 역학에서 '힘'이 만드는 속도의 물리적 현상과 일치한다.
장 이론
Field
필드(장, field): 공간 상의 각 지점마다 다른 값을 갖는 물리량
- 스칼라장(scalar field): 공간의 모든 점에 스칼라량이 대응된 장 e.g. 온도 분포, 호수의 수압 분포, 공간 전위, 위치에너지 등
- 벡터장(vector field): 공간의 모든 점에 벡터량이 대응된 장 e.g. 공기의 움직임, 유체 속도장, 전기장, 자기장, 중력장 등
- 두 장의 수학적 정의는 다음과 같다.
- 스칼라장: 정의역 A의 모든 원소 x에 스칼라 F(x)를 대응시킨다.
- 벡터장: 정의역 A의 모든 원소 x에 벡터 F(x)를 대응시킨다.
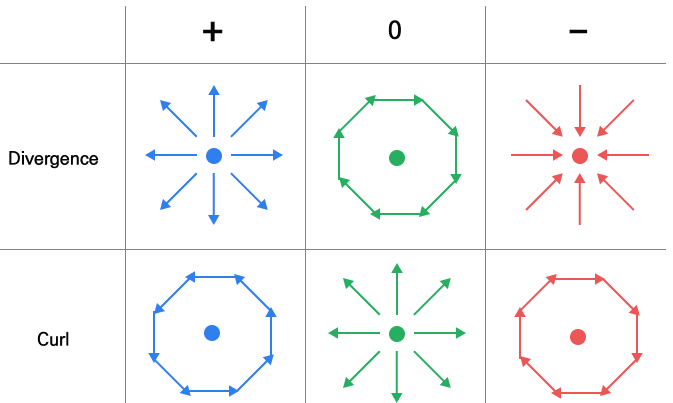
필드는 발산과 회전의 유형 및 부호에 따라 그 모양과 특성[그림 2]이 달라지는데, 이후 물리학적 현상을 확인하면서 자세히 살펴보도록 한다.
|
발산
|
비발산
|
|
|
회전
|
발산-회전장
|
비발산-회전장
|
|
비회전
|
발산-비회전장
|
비발산-비회전장
|
만유인력
Gravitational Force
Newton은 1687년 지구와 달 사이에 작용하는 힘에 관한 일련의 증명을 『자연철학의 수학적 원리(프린키피아)(Philosophiae Naturalis Principia Mathematica)』에서 최초로 언급하였다. 지금의 현대적 해석과는 달리 원래 프린키피아에서는 (1)다양한 궤도(원, 타원)를 가질 수 있는 행성의 움직임을 (2)구심력 개념을 도입하여 (3)기하학과 비례식만으로 표현했는데, 결론에는 이 모든 것이 중력 때문임을 밝혔기 때문에 아래의 문장이 가장 유명해졌다.
- 동양에는 나가사키 출신의 일본인 천문학자 시즈키 타다오(Shizuki Tadao, 1760-1806)가 네덜란드어로 적힌 뉴턴역학을 번역하면서 '만유인력'이라는 단어로 소개되었다.
만유인력의 법칙
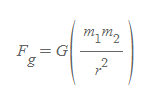
■
의미: 우주의 모든 입자는 다른 모든 입자를 끌어당기며, 그 인력은 두 입자의 질량에 곱에 비례하고, 그들 사이의 거리의 제곱에는 반비례한다.

- 만유인력의 법칙은 만유인력의 크기를 정리한 식으로 방향은 [그림 3]과 같이 항상 두 물체가 서로 끌어당기는 방향이다.
- G는 만유인력 상수 값이고, 잉글랜드의 자연철학자 캐번디시(Henry Cavendish, 1731-1810)가 후에 실험적으로 값을 규명했다.
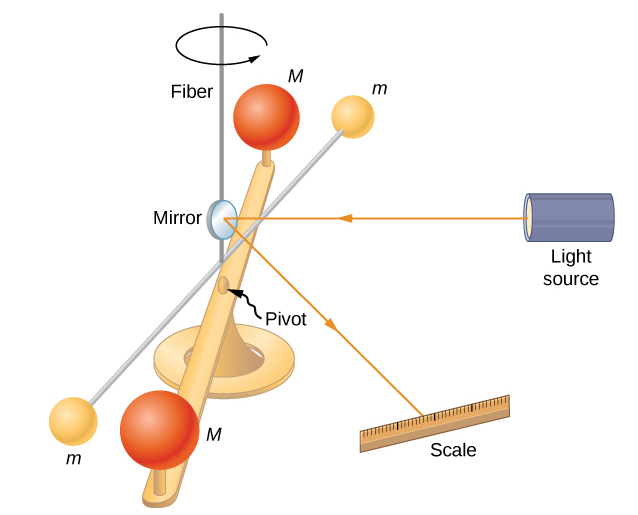
[1] [그림 4]와 같은 캐번디시 실험장치에 달린 질량이 작은 구들은 만유인력에 의해 질량이 큰 구 쪽으로 가속한다.
[2] 이들이 가속할 때 연직의 수정섬유(fiber)가 비틀리게 된다.
[3] 수정섬유가 비틀려 작용하는 탄성력과 질량 사이의 중력이 균형을 이룰 때 작은 구들은 새로운 평형위치에 도달한다.
[4] 광원을 이용하여 빛의 편향도(크기)를 잰다. 빛 편향의 크기는 수정섬유가 비틀린 정도에 비례하여 나타난다.
Cavendish는 자신의 실험장치로 중력을 측정하여 만유인력 상수 G의 값을 구하였다.
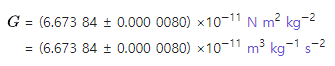
- 현대에는 만유인력 상수 G를 대략 6.673×10^-11[N·m2·kg^-2]로 근사하여 사용한다.
'물리학 > 고전역학' 카테고리의 다른 글
| 【2022 물리학 | 고전역학】 뉴턴의 운동법칙: 가속도와 작용-반작용 (0) | 2022.01.08 |
|---|---|
| 【2022 물리학 | 고전역학】 뉴턴의 운동법칙: 힘과 관성의 법칙 (0) | 2022.01.07 |
| 【2022 물리학 | 고전역학】 n-차원 상에서의 운동 2 | 포물선 운동, 포물체 운동 (0) | 2022.01.03 |
| [물리학-고전역학] 자유낙하물체 | Freely Falling Objects (0) | 2022.01.02 |
| 【2022 물리학 | 고전역학】 일차원 상에서의 운동 2 | 등가속도 운동 공식 유도 (0) | 2022.01.01 |




