[고전역학_물체의 운동]에서 배운 물체의 운동 지식을 바탕으로 다양한 중력장 운동의 경우를 다루도록 한다.
갈릴레이의 사고 실험
Galilei's Thought Experiment
이탈리아의 위대한 철학자이자 물리학자인 갈릴레이(Galileo Galilei, 1564~1642)는 근대 과학의 아버지로서 '사고실험(thought experiment)'을 통해 종래의 아리스토텔레스의 자유낙하 이론에 대해 반박하였다. 사고 실험이란, 현실적으로 구현할 수 없는 실험일지라도 이상적인 조건 하를(under ideal circumstances) 최대한 '조성(shaping)' 및 '사고(thoughts)'하면서 실험 결과를 도출하는 일련의 과정을 의미한다.
[1] 아리스토텔레스에 따르면 무거운 물체일수록 먼저 땅에 떨어진다. 만약 이를 맞다고 가정하면, 무거운 물체 A와 가벼운 물체 B가 존재하는 경우, A가 B보다 빨리 떨어질 것이다.
[2] 만약 A와 B를 묶는다면, 두 물체의 속성에 따라 (1)A는 빨리 떨어지려고 할 것이고, (2)B는 천천히 떨어지려고 할 것이다. 아리스토텔레스의 이론에 따르면, 이 둘을 묶은 낙하 결과는 두 물체의 낙하 속력의 평균 값을 가지게 될 것이다.
[3] 하지만 동시에 두 물체의 무게는 더욱 무거워져 더 빨리 떨어지는 결과를 보인다. 즉, 물체의 낙하 속력은 물체의 무게 속성에 기인하지 않는다고 할 수 있다.
위의 유명한 사고 실험은 하나의 가정에서 상반된 두 가지 결론이 나와 애초에 가정이 틀림을 보여 준다.
갈릴레이는 이후 자신이 고안한 실험을 통해 공기의 저항이 없는 조건[그림 1]에서, 지표면 부근의 모든 물체는 질량과 관계없이 동등한 중력가속도를 가진다고 생각했다. ⇒ 지구의 중력에 의해 물체는 일정한 높이에서 중력가속도라는 등가속도를 가지며, 중력가속도 g의 방향은 항상 지구중심부를 향한다.
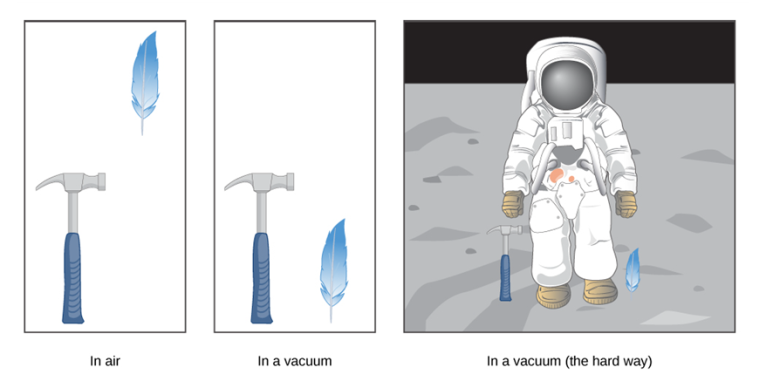
자유낙하(free fall): 공기저항이 부재한 조건에서, 지표면으로 떨어지는 물체의 가속도운동
- 1971년 8월 2일, 미국의 우주비행사 데이비드 스콧(David Scott, 1932~, 공학자)이 깃털-망치 낙하실험을 수행[그림 2]하였다. 달에서의 자유낙하실험 결과 깃털과 망치는 달 표면에 거의 동시에 떨어졌다.
자유낙하가속도: 벡터 g로 표현하며, 크기는 g, 지표면을 기준으로 방향은 지구 중심부를 향한다.
- g는 고도가 높아짐에 따라 감소한다.
- g는 질량분포에 기인하기 때문에, 위도에 따라서도 크기가 약간씩 달라진다. ⇒ 지구의 실제 모양은 완전한 구체가 아닌 타원이고, 적도가 극지방보다 좀 더 두툼하다.
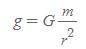
- 물리량
- G: 만유인력 상수
- m: 중력장을 생성하는 질량
- r: 중력장의 원전 질량으로부터 특정한 점까지 떨어진 거리
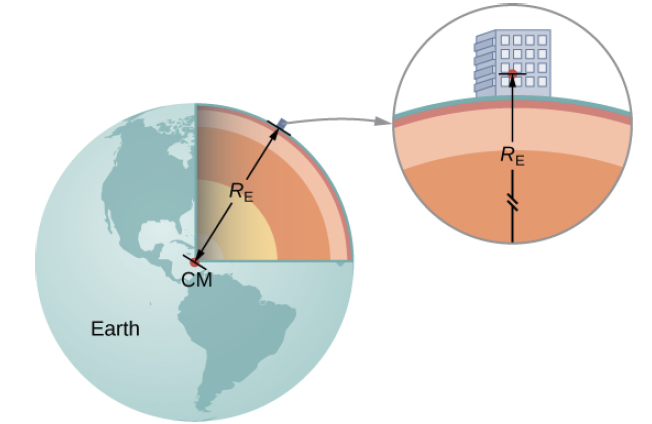
중력장 식에서 m은 지구 질량(M_E)을, r은 지구의 반지름(R_E)을 대입함[그림 3]으로써 중력 가속도의 크기를 9.8[m/s^2]으로 구할 수 있다.
- M_E는 약 5.95×10^24[kg]이다.
- R_E는 약 6.4×10^6[m]이다.
자유낙하물체: 처음의 운동 상태와는 무관하게 중력만의 영향 하에 자유롭게 움직이는 물체로 아래와 같은 조건에서 물체는 자유낙하 한다.
- 연직하방물체: (위에서) 아래로 떨어뜨리는 물체
- 연직상방물체: (아래에서) 위로 던진 물체
- 포물체
중력가속도의 크기
■
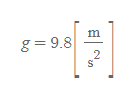
이를 운동학 식에 대입할 경우, 가속도이므로 a_y=-g를 대입해야 한다.
- 자유낙하물체는 운동이 연직방향(y축)으로 발생하고, 가속도는 지표면 방향인 아래 방향으로 크기를 가지기 때문에 (-)부호가 반드시 필요하다.
자유낙하 조건에서 운동학 식
■
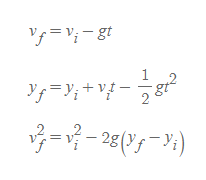
자유낙하 조건에서 운동학 식
[1] 운동학 식
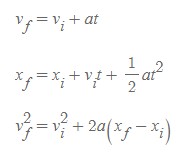
[2] y축으로 변경
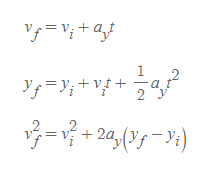
[3] a_y = -g로 대입한다.
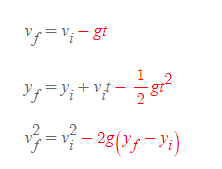
q.e.d.
실제 운동학 식 대입 시, a_y가 -g로 치환됨으로써 바뀐 부호에 유의하도록 한다.
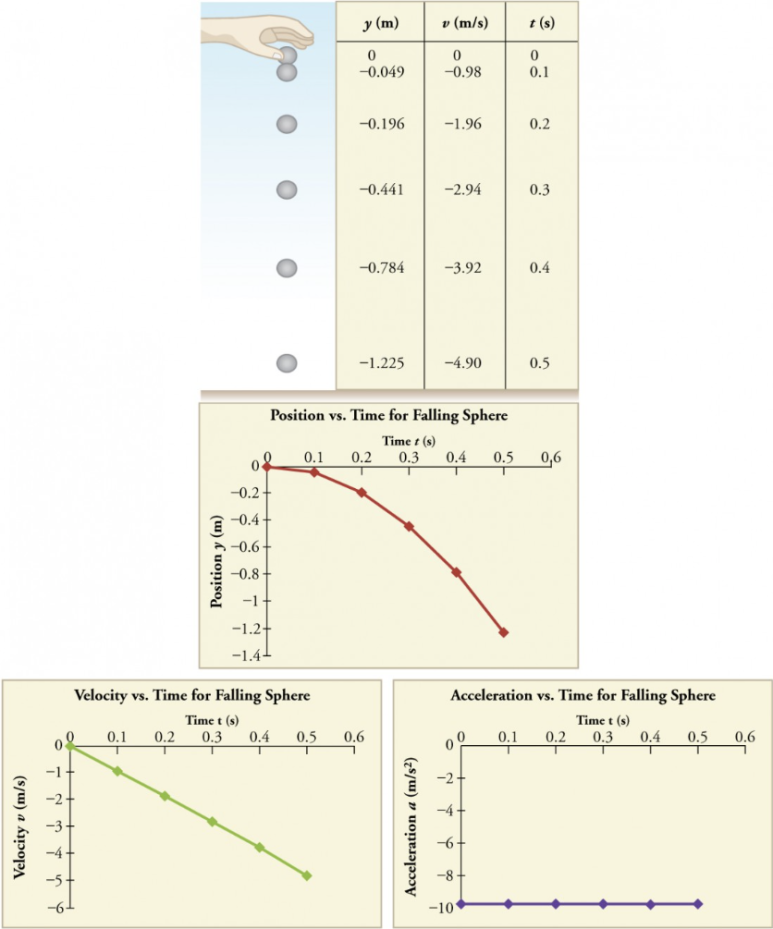
위의 공식 이외에도 그래프[그림 4]와 같이 운동 내용을 표현함으로써, 기하적으로 운동 결과(최종 속력, 도달 시간, 도달 거리 등)를 구할 수도 있다.
'고급물리학 > 고전역학' 카테고리의 다른 글
| [물리학-고전역학] 뉴턴의 발견 - 중력의 법칙 | Law of Gravity (0) | 2022.01.03 |
|---|---|
| 【2022 물리학 | 고전역학】 n-차원 상에서의 운동 2 | 포물선 운동, 포물체 운동 (0) | 2022.01.03 |
| 【2022 물리학 | 고전역학】 일차원 상에서의 운동 2 | 등가속도 운동 공식 유도 (0) | 2022.01.01 |
| 【2022 물리학 | 고전역학】 일차원 상에서의 운동 1 (0) | 2022.01.01 |
| 【2022 물리학 | 고전역학】 벡터 Vectors (0) | 2021.12.19 |