[물리학-전자기학] 22. 유전체 | Dielectric

 

유전체(dielectric): 축전기의 도체 판 사이에 있는 부도체 물질로, 가장 일반적인 축전기의 경우 절연물질인 마일라(Mylar: 강화 폴리에틸렌 필름)와 같은 얇은 플라스틱 종이[그림 1]가 평행판 사이에 채워져 있다.

• 마일라: 본래는 강화 폴리에틸렌의 브랜드 이름으로 폴리에스터 물질의 실제 이름은 BoPET(biaxially oriented polyethylene terephthalate)이다. 1950년대 중반 듀폰(DuPont) 사에서 발명되었다.

 

그림 1. BoPET 필름

 

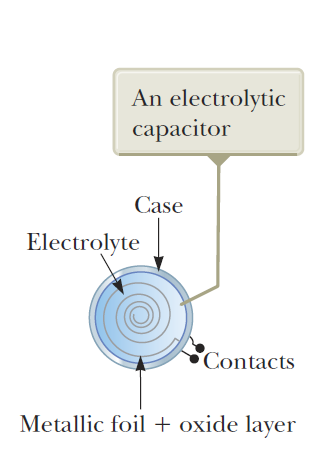
고형 유전체

• 고형 유전체를 사용함으로써 큰 금속 판막이 매우 작은 간격을 유지하면서도 서로 닿지 않는 기술적인 문제를 해결했다.
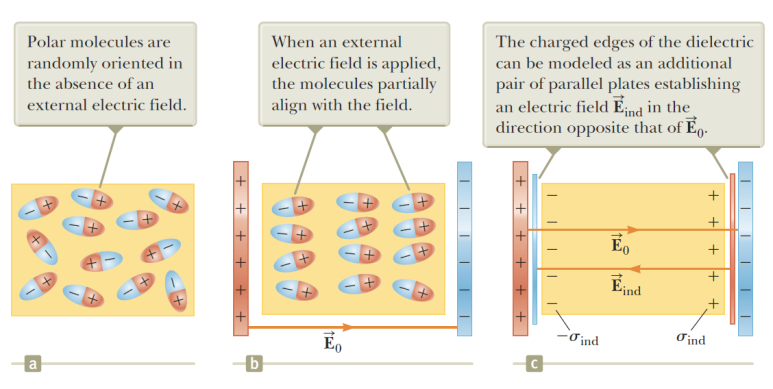
• 고형 유전체 내의 분극화는 [그림 2]와 같은 과정으로 진행된다. 두 도체판 사이의 전기장에 의해 유전체의 분자는 아래와 같이 일정한 극성 배열을 이룬다.
• 도체 판 사이의 전위차에 대한 최대 허용치를 확대 ⇒ 더 많은 전하와 에너지를 수용할 수 있다.
• 축전기의 크기가 동일할 때 속이 진공인 도체판보다 유전체로 찬 도체판의 전기용량이 더 크다. cf. 유전파괴(dielectric breakdown: 매우 큰 전기장에 유전체가 놓일 시, 부분적인 이온화에 의해 유전체 내에 전기가 흐른다.)

 

그림 2. 두 도체 내의 고형 유전체의 분극화 [출처: Principles of Physics, Serway & Jewett, 12th ed., 2012, p.683]

 

유전체가 없는 축전기의 전기용량

​​​

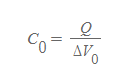
유전체가 있는 축전기의 전기용량

 

​​

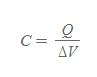
유전상수

​

■

​

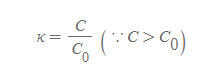
• 유전상수 κ(카파)는 축전기 내의 고형 유전체의 전하량 저장 능력[표 1]을 나타낸다.

 

표 1. 물질의 유전상수 표 [출처: University Physics Volume 2, OpenStax, 2016, p.384]

 

​

전기용량의 식에 따라 축전기에 전하량이 일정한 양을 가질 경우, 다음과 같이 구할 수도 있다.

​

​유전상수

​

■

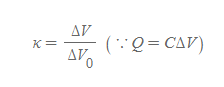
• C는 항상 C_0보다 크기 때문에, 유전상수는 반드시 1보다 크다.
• 유전상수는 무차원 상수이다.

​

[표 1]에서 물은 매우 큰 유전상수를 가지고 있다. 하지만 실제 축전기 제작에 물은 유전체로서 고려 대상이 아닌데, 그 이유는 물의 성질 중 하나인 이온을 쉽게 녹이는 특성이 도체 판 사이의 전하를 움직여 축전기를 방전시키기 때문이다.

​

실제 존재하는 유전체는 완벽한 절연체가 아니지 때문에 유전체로 채워진 도체 판 사이에 약간의 누설 전류(leak current)가 발생한다. ⇒ 누설 전류가 오랫동안 흐르게 되면 유도 시 사용된 전하량의 크기가 상당히 변하게 된다. 이러한 이유 때문에 축전기의 등가 전기용량 식은 오랜 시간 사용한 축전기에는 적합하지 않다.

​

 

유도전하와 분극

유전체를 넣은 도체 판 사이의 전위차는 다음과 같이 계산할 수 있다.

​​

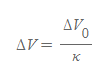
그러므로 도체판 사이의 전기장도 같은 비율로 감소하게 된다.

​

유전체를 넣은 도체 판 사이의 전위차

​​

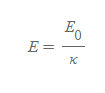
• 유전체가 있을 때 전기장의 세기가 감소한다. ⇒ 전기장을 발생시키는 표면 전하 밀도 σ가 더 작아진다.
• 도체판 위의 표면전하는 변하지 않는다. 그러나 반대 부호로 유도된 전하가 유전체의 표면에 발생한다. → 유전체 전체는 여전히 전기적으로 중성이나 유전체의 기하학적인 부분은 인접한 도체판의 전하와 반대되는 전하를 가진다.
• 분극현상(polarization): 부도체의 기하학적 양전하-음전하 재배치(재분배) 현상
• 유도 표면전하는 대체로 물질 내의 전기장 세기와 정비례 관계다. cf. 단, 유전체가 특정 결정체 혹은 매우 강한 전기장 속에 놓인 경우 정비례 관계는 깨진다.

$E_0=\frac{\sigma }{\epsilon _0}\ \to \ \textcolor{#0078cb}{E=\frac{\sigma -\sigma _i}{\epsilon _0}}\ \left(\because \sigma _i:\ 유전체\ 표면에\ 유도된\ 유도표면전하밀도\right)$E0​=σε0​​ → E=σ−σi​ε0​​ (∵σi​: 유전체 표면에 유도된 유도표면전하밀도)​

σ는 유전체가 없는 곳에서 평행판이 가진 표면 전하 밀도이고 유도 표면 전하 밀도와는 정반대 방향으로 전기장을 방출한다. ⇒ 도체판에서의 알짜 표면 전하 밀도는 표면 전하 밀도에 유도 표면 전하 밀도를 뺀 값(σ-σ_i)이다.

​

그러므로

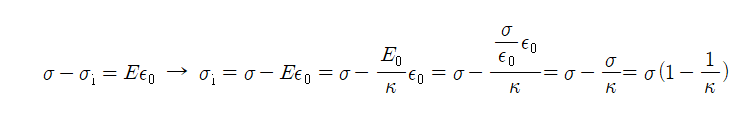
유전체의 유도표면전하밀도

 

■

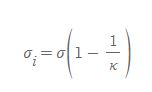
• 의미: 유전상수 κ의 값이 클수록 표면전하밀도와 유도표면전하밀도는 거의 같은 값을 가진다.

​

유전율

$\epsilon =\kappa \epsilon _0$ε=κε0​​

■