Herald-Lab

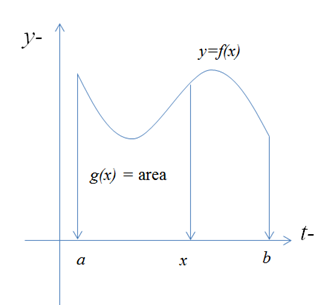
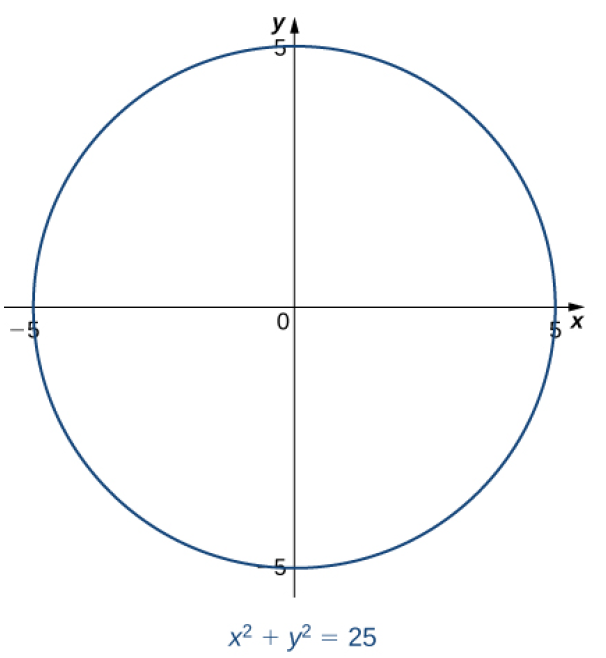
적분법에 들어가기에 앞서 먼저 미적분학의 미분법에 대해 간단히 복습하자. 미분법과 마찬가지로 적분에서도 합성함수를 적분하는 여러 가지 전략이 있다. 곱법칙(몫법칙을 포함해), 그리고 연쇄법칙과 대응되는(corresponds to) 적분법들도 존재하는데 대응관계는 다음과 같다. 1. 부분적분(integration by parts): 곱법칙에 대응한다. 2. 치환적분(integration by substitution): 연쇄법칙에 대응한다. 치환적분 치환적분은 연쇄법칙과 유사한 방법의 적분법으로 연쇄법칙에서의 내부함수의 치환 요령을 따른다. [1] 내부함수를 u로 치환한다. [2] du/dx=g'(x)를 구한다. [3] 적분식에서 dx를 다음과 같이 바꿔 쓸 수 있다. ⇒ dx=du/g'(x) [4] u를 ..

미적분학의 기본정리 2에서 F는 f에 대한 임의의 원시함수였고, F는 다시 ∫f(x)dx로 표현할 수 있다. - 원시함수는 부정적분(indefinite integral)이라 불리며, 함수족(family)이다. ⇒ 즉, 부정적분은 하나의 함수족이다. F(x)=x^3/3은 f(x)=x^2의 역도함수, 즉 부정적분이며 여러 개의 부정적분을 갖는다. - c는 부정적분의 상수(constant of integral)이다. - 부정적분의 상수는 임의의 값을 갖는다. 자주 사용되는 함수-부정적분 공식 함수의 미분공식처럼 앞으로 적분을 풀기 위해서는 부정적분표가 필요하다. 부정적분의 여러 공식은 우변의 함수를 미분하여 피적분함수를 구하는 것으로 증명할 수 있다. ※ List of Integrals There are ni..

뉴턴의 스승 배로(Isaac Barrow, 1630~1677, 잉글랜드)는 미분 문제와 적분 문제가 서로 밀접함을 발견했다. - 배로는 접선 문제와 넓이 문제의 풀이가 서로 역과정임을 확인했다. ⇒ 미적분학의 기본정리 이전에 적분은 합의 극한으로서 계산되었다. 함수 f가 구간 [a, b]에서 적분가능하고 Δx=b-a/n, x_i=a+iΔx일 때, 정적분은 다음과 같이 정의한다. 미적분학의 기본정리 미적분학의 기본정리 1(Fundamental Theorem of Calculus 1, FTC1) 만약 f가 구간 [a, b]에서 연속한다면, 로 정의된 함수 g는 구간 [a, b]에서 연속이고, 구간 (a, b)에서 미분가능하며, g'(x)=f(x)이다. ■ - g(x)는 f(t)의 넓이와 같다. - g는 적분..

곡선함수의 넓이를 구할 때, 직사각형의 넓이를 설정하는 방법으로 2가지 근사와 함께 표본점을 이용한 극한 값까지 확인했다. 특히 표본점의 근사식은 곡선의 길이, 입체의 부피, 질중심, 압력에 의한 힘(force) 등 다양한 물리량을 구하는 문제 등에 활용된다. 그러므로 이러한 형태의 극한은 특별한 이름과 기호를 붙일 수 있다. 정적분 ■ 만일 f가 a≤x≤b에서 정의된 연속함수라면, 구간 [a, b]를 동일한 폭 Δx=b-a/n인 n개의 부분 구간들로 나눌 수 있다. x_0=a, x_1, x_1, ..., x_n=b까지를 부분구간들의 끝점으로 두고 x_1*, x_2*, ..., x_n*을 임의의 표본점이라 하면, x_i*는 i번째의 부분구간 [x_i-1, x_i]에 놓이게 된다. 그러면 a에서 b까지의 ..

적분의 기원 적분의 기원은 고대 그리스 시대의 수학자 아르키메데스(시라쿠사 출신)가 곡선을 가진 도형의 면적과 부피를 구함에 있어, 오늘날의 적분과 유사한 방법을 사용한 데서 출발한다. 이후 1622년 이탈리아의 수학자 카발리에리(Bonaventura Francesco Cavalieri; 밀라노 출신)가 무한의 개념을 도입해, 곡선으로 둘러싼 도형의 면적은 매우 폭이 좁은 직사각형들의 면적의 합이라는 주장을 한다. ※ 참고: [미분] 1장. 들어가기: 미분적분학 https://herald-lab.tistory.com/2 [미분] 1장. 들어가기: 미분적분학 미분적분학(calculus): 함수로 표현할 수 있는 어떤 물리량의 변화를 분석하는 데 사용되는 수학의 한 기법 - 함수가 그래프로 표현될 때, 특정..

음함수 미분법 지금까지 미분법을 위한 함수는 y=f(x)의 꼴을 가졌다. 즉, 우변에 x항을 모두 모은 형태로 이전 장까지는 양함수(explicit function)에 대한 미분법만을 다루었다. - where the variable y is on the left side, and the right side depends only on the independent variable x, then the function is said to be an explicit function(or be given explicitly). 그러나, 와 같은 함수는 y=f(x) 꼴로 y를 표현할 수 없다. 즉, 식 10.1은 음함수적(implicitly)으로 표현될 수 있다고 정의한다. 음함수를 정의하기 위해 식 10.2를 ..

지수함수(exponential function): 거듭제곱의 지수를 변수로, 정의역을 실수 전체로 정의하는 초월함수 로그함수(logarithm, 대수함수): 지수함수의 역함수로, 어떤 수를 나타내기 위해 고정된 밑(base)을 몇 번 곱해야 하는 지 나타내는 함수 - 로그함수의 지수함수적 정의: a>0, a≠1이고, y>0일 때, x, y 사이에 y=a^x라는 관계가 있을 때, 'x는 a를 밑으로 하는 y의 로그(대수)'라 하고 로 표기한다. - a≠1인 이유는 1의 거듭제곱이 모두 1이기 때문에, 지수에 어떤 값이 오더라도 1이 되어 무의미하기 때문이다. - x 값의 범위는 모든 실수이다. ⇒ 실수를 로그를 통해 나타낼 수 있다. 지수와 로그의 기본성질 지수의 기본성질 ■ 여기서 e의 정의는 다음과 같..

삼각함수(trigonometric function): 각도와 관련된 여러가지 함수 - 삼각함수는 기본적으로 3가지 함수-sine 함수, cosine 함수, tangent 함수-가 있으며, 이들의 역수-cosecant, secant, cotangent-를 모두 합치면 총 6개이다. 삼각함수의 정의 삼각함수는 먼저 직각삼각형을 통해 다음과 같이 정의할 수 있다. 삼각함수의 직각삼각형 정의의 역수는 각각 코시컨트, 시컨트, 그리고 코탄젠트의 정의와 같다. 또한 단위원(unit circle; 반지름 r이 1인 원으로 원점 (0, 0)을 중심으로 한다.)으로 삼각함수를 정의할 수도 있다. 반지름을 r이라 둘 때, 각 삼각함수의 정의는 다음과 같이 정리한다. 1. sinθ = y/r 2. cosθ = x/r 3. ..

곱법칙 함수(구함수) f와 g가 모두 미분가능일 때, 함수들을 곱하거나 나누어 얻어지는 새로운 함수의 도함수 역시 구할 수 있다. 먼저, 곱법칙(product rule)은 두 구함수를 곱하여 얻은 새로운 함수의 도함수를 구하는 방법이다. 곱법칙 ■ - 두 함수의 곱의 도함수는 앞의 함수에 뒤의 함수의 도함수를 곱한 값에, 뒤의 함수에 앞의 함수의 도함수를 곱한 값 둘을 더한 것과 같다. 몫법칙 한편, 몫법칙(quotient rule)은 두 함수를 나누어 얻은 새로운 함수의 도함수를 구하는 방법이다. 몫법칙 ■ 연쇄법칙 연쇄법칙은 합성함수(composition of two functions)를 미분하는 방법이다. 만약, 와 같은 함수를 미분할 경우, 지금까지 배운 미분공식으로는 이를 풀 수 없을 것이다. ..

자주 사용되는 함수-미분 공식 중 다항함수와 관련된 것들을 살펴보자. 1. 상수함수 모든 함수 중 상수함수는 가장 간단한 함수이다. 상수함수의 도함수 ■ - d/dx는 미분연산자로 뒤에 나타난 함수를 미분한다는 뜻이다. PROOF. 상수함수의 도함수 ■ 2. 거듭제곱함수 함수 f(x)=x^n의 n이 1이면, x^1=x이고, 그래프는 직선 f(x)=x로 그려진다. 이것의 기울기는 1이고, 따라서 다음과 같이 쓸 수 있다. dx^1/dx=1 x가 2, 3일 때, 대입하면 2x, 3x^2인 것을 알 수 있다. 식 6.1을 양의 거듭제곱 법칙이라 하고, 증명은 다음과 같다. PROOF. 양의 거듭제곱 법칙 ■ 음의 정수를 지수로 갖는 거듭제곱의 도함수도 역시 거듭제곱의 법칙(power rule)이 성립한다. 따..